
 如图,在平面直角坐标系中,已知抛物线y=x2-bx+c经过A(0,3),B(1,0)两点,顶点为M.
如图,在平面直角坐标系中,已知抛物线y=x2-bx+c经过A(0,3),B(1,0)两点,顶点为M.分析 (1)直接将已知点的坐标代入到二次函数的解析式中求得未知系数的值即可;
(2)根据A、B两点的坐标可以求得OA和OB的长,然后根据旋转的性质求得点C的坐标,然后向下平移2个单位即可得到平移后的抛物线的解析式.
解答 解:(1)已知抛物线y=x2-bx+c经过A(0,3),B(1,0)两点,
∴$\left\{\begin{array}{l}{3=c}\\{0=1-b+c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$,
∴b、c的值分别为4,3.
故答案是:4;3.
(2)∵A(0,3),B(1,0),
∴OA=3,OB=1.
∴旋转后C点的坐标为(4,1).
当x=4时,y=x2-4x+3=42-4×4+3=3,
∴抛物线y=x2-4x+3经过点(4,3).
∴将原抛物线沿y轴向下平移2个单位后过点C.
∴平移后的抛物线解析式为y=x2-4x+1.
点评 此题主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
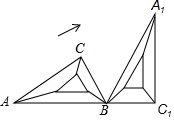 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针转动一个角度到A1BCl的位置,使得点A,B,C1在同一条直线上,那么这个旋转角的度数等于120°.
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针转动一个角度到A1BCl的位置,使得点A,B,C1在同一条直线上,那么这个旋转角的度数等于120°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB=CD,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知AB=CD,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | MB=ND | C. | AM=CN | D. | AM∥CN |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
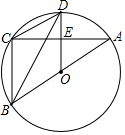 如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且OD⊥AC于点E,连结BD、CD.
如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且OD⊥AC于点E,连结BD、CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com