
【题目】如图,已知点![]() 经过原点
经过原点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .点
.点![]() 在
在![]() 上,
上,![]() ,圆心
,圆心![]() 的坐标为__________.
的坐标为__________.
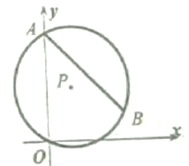
【答案】![]()
【解析】
连接OP,OB,PB,延长BP交⊙P于E,连接OE,作EF⊥OA于F,BH⊥x轴于H.利用全等三角形的性质求出点E坐标即可解决问题.
解:连接OP,OB,PB,延长BP交⊙P于E,连接OE,作EF⊥OA于F,BH⊥x轴于H.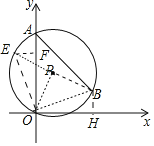
∵∠BPO=2∠BAO,∠BAO=45°,
∴∠BPO=90°,
∵PO=OB,
∴△PBO是等腰直角三角形,
∵BE是直径,
∴∠BOE=90°,
∴∠OBE=∠OEB=45°,
∴OE=OB,
∵∠EOB=∠AOH=90°,
∴∠EOF=∠BOH,
∵∠EFO=∠BHO=90°,
∴△EFO≌△BHO(AAS),
∴OF=OH=5,EF=BH=2,
∴E(2,5),
∵PE=PB,
∴P![]() .
.
故答案为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某地准备围建一个矩形苗圃园,其中一边靠墙,另外三边用周长为30米的篱笆围成.已知墙长为![]() 米,设苗圃园垂直于墙的一边长为
米,设苗圃园垂直于墙的一边长为![]() 米,苗圃园的面积为
米,苗圃园的面积为![]() 平方米.
平方米.
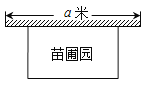
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
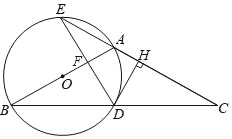
(1)求证:DH是圆O的切线;
(2)若![]() =
=![]() ,求证A为EH的中点;
,求证A为EH的中点;
(3)若EA=EF=2,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,通过画图发现,无论
,通过画图发现,无论![]() 取何值,抛物线总会经过两个定点
取何值,抛物线总会经过两个定点
![]() 直接写出这两个定点的坐标 、 ;
直接写出这两个定点的坐标 、 ;
![]() 若将此抛物线向右平移
若将此抛物线向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
个单位,平移后的抛物线顶点都在某个函数的图象上,求这个新函数的解析式(不必写自变量取值范围);
![]() 若抛物线
若抛物线![]() 与直线
与直线![]() 有两个交点
有两个交点![]() 与
与![]() .且
.且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,E,F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确都有( )个.
①QB=QF;②AE⊥BF;③![]() ;④
;④![]() ;④S四边形ECFG=2S△BGE
;④S四边形ECFG=2S△BGE

A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,![]() ≈1.414,
≈1.414,![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c(a≠0)的图象如图,给出下列4个结论:①abc>0; ②b2>4ac; ③4a+2b+c>0;④2a+b=0.其中正确的有( )个.
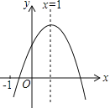
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com