练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图，已知一块圆心角为270°的扇形铁皮，用它作一个圆锥形的烟囱帽（接缝忽略不计），圆锥底面圆的直径是60cm，则这块扇形铁皮的半径是（　　）
    A．40cmB．50cmC．60cmD．80cm

    分析 首先根据圆锥的底面直径求得圆锥的底面周长，然后根据底面周长等于展开扇形的弧长求得铁皮的半径即可．

    解答 解：∵圆锥的底面直径为60cm，
    ∴圆锥的底面周长为60πcm，
    ∴扇形的弧长为60πcm，
    设扇形的半径为r，
    则$\frac{270πr}{180}$=60π，
    解得：r=40cm，
    故选A．

    点评 本题考查了圆锥的计算，解题的关键是首先求得圆锥的底面周长，利用圆锥的底面周长等于扇形的弧长求解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    1．如图，已知点B，D在反比例函数y=$\frac{a}{x}$（a＞0）的图象上，点A，C在反比例函数y=$\frac{b}{x}$（b＜0）的图象上，AB∥CD∥x轴，AB，CD在x轴的同侧，AB=4，CD=3，AB与CD的距离为1，则a-b的值是12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在一个口袋中有4个完全相同的小球，把它们分别标号1、2、3、4．小明先随机地摸出一个小球，小强再随机地摸出一个小球．记小明摸出球的标号为x，小强摸出的球标号为y．小明和小强在此基础上共同协商一个游戏规则：当x＞y时小明获胜，否则小强获胜．
    （1）若小明摸出的球不放回，求小明获胜的概率．
    （2）若小明摸出的球放回后小强再随机摸球，问他们制定的游戏规则公平吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

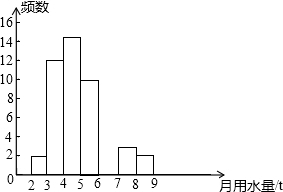    19．小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）．
    月均用水量（单位：t）频数百分比
    2≤x＜324%
    3≤x＜41224%
    4≤x＜51530%
    5≤x＜61020%
    6≤x＜7612%
    7≤x＜836%
    8≤x＜924%
    （1）请根据题中已有的信息补全频数分布表和频数分布直方图；
    （2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你估计总体小王所居住的小区中等用水量家庭大约有多少户？
    （3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列举法（画树状图或列表）求抽取出的2个家庭来自不同范围的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

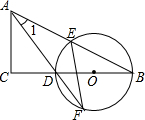    6．如图，在△ABC中，∠C=90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF．
    （1）求证：∠1=∠F．
    （2）若sinB=$\frac{\sqrt{5}}{5}$，EF=2$\sqrt{5}$，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．学生甲与学生乙学习概率初步知识后设计了如下游戏：学生甲手中有6，8，10三张扑克牌，学生乙手中有5，7，9三张扑克牌，每人从各自手中取一张牌进行比较，数字大的为本局获胜，每次取的牌不能放回．
    （1）若每人随机取手中的一张牌进行比赛，请列举出所有情况，并求学生乙本局获胜的概率；
    （2）若比赛采用三局两胜制，即胜2局或3局者为本次比赛获胜者，当学生甲的三张牌出牌顺序为先出6，再出8，最后出10时，学生乙随机出牌应对，求学生乙本次比赛获胜的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．在“春节”期间，加开从赣州到南昌的豪华旅游列车，途中停靠站为泰和、吉安，现有互不认识的甲，乙两人从赣州上车．
    （1）求甲在吉安下车的概率．
    （2）用树形图或列表法求甲乙两人中至少有一人在吉安站下车的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，矩形ABCD中，AD=3，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是3$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．已知等式（x+a）（x+b）=x2-x+ab，则a+b的值是-1．

    查看答案和解析>>

    同步练习册答案