
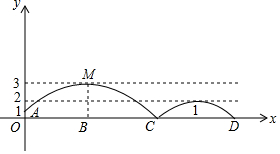
 如图,需在一面墙上绘制两个形状相同的抛物绒型图案,按照图中的直角坐标系,最高点M到横轴的距离是4米,到纵轴的距离是6米;纵轴上的点A到横轴的距离是1米,右侧抛物线的最大高度是左侧抛物线最大高度的一半.(结果保留整数或分数,参考数据:$\sqrt{3}$=$\frac{7}{4}$,$\sqrt{6}$=$\frac{5}{2}$)
如图,需在一面墙上绘制两个形状相同的抛物绒型图案,按照图中的直角坐标系,最高点M到横轴的距离是4米,到纵轴的距离是6米;纵轴上的点A到横轴的距离是1米,右侧抛物线的最大高度是左侧抛物线最大高度的一半.(结果保留整数或分数,参考数据:$\sqrt{3}$=$\frac{7}{4}$,$\sqrt{6}$=$\frac{5}{2}$)分析 (1)根据已知条件得到M(6,4),设左侧抛物线的表达式为y=a(x-6)2+4,把A(0,1)代入y=a(x-6)2+4即可得到结论;
(2)根据(1)中的结论设右侧抛物线的表达式为y=-$\frac{1}{12}$(x-h)2+2,把C(13,0)代入y=-$\frac{1}{12}$(x-h)2+2即可得到结论;
(3)求出D(23,0),于是得到结论.
解答 解:(1)∵最高点M到横轴的距离是4米,到纵轴的距离是6米
∴M(6,4),
设左侧抛物线的表达式为y=a(x-6)2+4,
把A(0,1)代入y=a(x-6)2+4得a=-$\frac{1}{12}$,
∴左侧抛物线的表达式为y=-$\frac{1}{12}$(x-6)2+4;
(2)∵抛物线y=-$\frac{1}{12}$(x-6)2+4与x轴的交点C(13,0),
∵右侧抛物线与左侧抛物线形状相同,
∴设右侧抛物线的表达式为y=-$\frac{1}{12}$(x-h)2+2,
把C(13,0)代入y=-$\frac{1}{12}$(x-h)2+2得0=-$\frac{1}{12}$(13-h)2+2,
解得:h=18,h=8(不合题意,舍去),
∴右侧抛物线的表达式为y=-$\frac{1}{12}$(x-18)2+2;
(3)∵C(13,0),右侧抛物线的对称轴是直线x=18,
∴D(23,0),
∴这个图案在水平方向上的最大跨度是23米.
点评 此题考查二次函数的实际运用,待定系数法求函数解析式,根据图象得出点的坐标是解决问题的关键.


科目:初中数学 来源: 题型:填空题
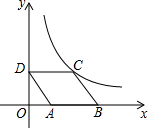 如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).
如图,?ABCD放置在平面直角坐标系中,已知点A(2,0),B(6,0),D(0,3),反比例函数的图象经过点C,将?ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,则点E的坐标为($\frac{12}{5}$,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
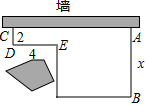 用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题:
用一段长为32m的篱芭绕过障碍物围成一个菜园,菜园一边靠墙.如图,已知CD=2m,DE=4m,设AB=x(m)(2<x<14),菜园面积为y(m2),请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
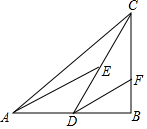 定义:有两条边长的比值为$\frac{1}{2}$的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.
定义:有两条边长的比值为$\frac{1}{2}$的直角三角形叫“潜力三角形”.如图,在△ABC中,∠B=90°,D是AB的中点,E是CD的中点,DF∥AE交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
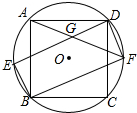 正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G.
正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
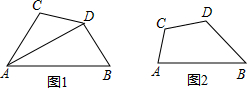 (1)如图1,已知AD平分∠BAC,若DB=DC,求证:∠ABD+∠ACD=180°;
(1)如图1,已知AD平分∠BAC,若DB=DC,求证:∠ABD+∠ACD=180°;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
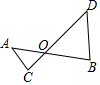 如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为50°;∠CAO是(填“是”或“不是”)∠AOC的同旁内角.
如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为50°;∠CAO是(填“是”或“不是”)∠AOC的同旁内角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com