
分析 根据x、y的值可以求得题目中所求式子的值.
解答 解:∵x=$\frac{1}{\sqrt{5}-2}$=$\sqrt{5}+2$,y=$\frac{1}{\sqrt{5}+2}$=$\sqrt{5}-2$,
∴$x-\frac{1}{x}$
=$\sqrt{5}+2-\frac{1}{\sqrt{5}+2}$
=$\sqrt{5}+2-(\sqrt{5}-2)$
=$\sqrt{5}+2-\sqrt{5}+2$
=4,
x2+y2-xy
=(x+y)2-3xy
=$(\sqrt{5}+2+\sqrt{5}-2)^{2}-3(\sqrt{5}+2)(\sqrt{5}-2)$
=$(2\sqrt{5})^{2}-3×1$
=20-3
=17.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2sinA-3=0 | B. | cos2B=1 | C. | tan B+1=0 | D. | tan2 A=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=bsinA | B. | a=bcosA | C. | a=btanA | D. | a=btanB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
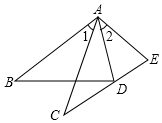 在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
在数学课上,林老师在黑板上画出如图所示的△ABD和△ACE两个三角形,并写出四个条件:①AB=AC;②AD=AE;③∠1=∠2;④∠B=∠C.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com