
【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当△ABP≌△ADN时,BP=4 ![]() ﹣4.
﹣4.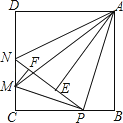
查看答案和解析>>
科目:初中数学 来源: 题型:
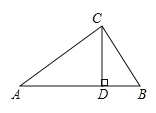
【题目】如图,∠ABD=90°,
(1)点B在直线 上,点D在直线 外;
(2)直线 与直线 相交于点A,点D是直线 与直线 的交点,也是直线 与直线 的交点,又是直线 与直线 的交点;
(3)直线 ⊥直线 ,垂足为点 ;
(4)过点D有且只有 条直线与直线AC垂直.
查看答案和解析>>
科目:初中数学 来源: 题型:
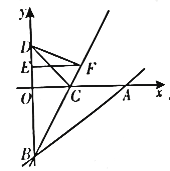
【题目】如图,在平面直角坐标系xOy中,直线![]() 交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将
交x轴正半轴于点A,交y轴负半轴于点B,点C在线段OA上,将![]() 沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
沿直线BC翻折,点A与y轴上的点D(0,4)恰好重合.
(1)求直线AB的表达式.
(2)已知点E(0,3),点P是直线BC上的一个动点(点P不与点B重合),连接PD,PE,当![]() PDE的周长取得最小值时,求点P的坐标。
PDE的周长取得最小值时,求点P的坐标。
(3)在坐标轴上是否存在一点H,使得![]() HAB和
HAB和![]() ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
ABC的面积相等?若存在,求出满足条件的点H的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(﹣2,﹣2).
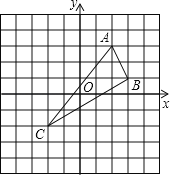
(1)请在图中作出△ABC关于直线x=﹣1的轴对称图形△DEF(A、B、C的对应点分别是D、E、F),并直接写出D、E、F的坐标;
(2)求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地某月1~20日中午12时的气温(单位:℃)如下:
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整:
气温分组(℃) | 划记 | 频数 |
12≤x<17 |
| 3 |
17≤x<22 | ________ | _______ |
22≤x<27 | _________ | ________ |
27≤x<32 |
| 2 |
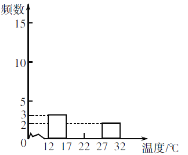
(2)补全频数分布直方图;
(3)根据频数分布表或频数分布直方图,分析数据的分布情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
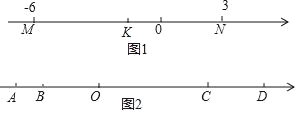
如图1,在数轴上点M表示的数是﹣6,点N表示的数是3,求线段MN的中点K所示的数.
对于求中点表示数的问题,只要用点N所表示的数3,加上点M所表示的数﹣6,得到的结果再除以2,就可以得到中点K所表示的数;即K点表示的数为![]() =﹣1.5
=﹣1.5
利用材料中知识解决下面问题:
如图2,已知数轴上有A、B、C、D四点,A点表示数为﹣6,B点表示的数是﹣4,线段AD=18,BC=3CD.
(1)点D所表示的数是 ;
(2)若点B以每秒4个单位的速度向右运动,点D以每秒1个单位的速度向左运动,同时运动t秒后,当点C为线段BD的中点时,求t的值;
(3)若(2)中点B、点D的运动速度运动方向不变,点A以每秒10个单位的速度向右运动,点C以每秒3个单位的速度向左运动,点P是线段AC的中点,点Q是线段BD的中点,A、B、C、D四点同时运动,运动时间为t,求线段PQ的长(用含t的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
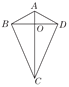
【题目】两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有_____(填序号).
①AC⊥BD;②AC,BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为![]() AC·BD.
AC·BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com