
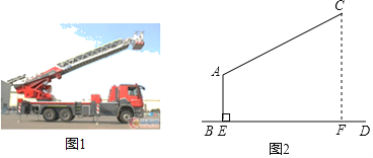
【题目】图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC是可伸缩的,其转动点A距离地面BD的高度AE为3.5m.当AC长度为9m,张角∠CAE为112°时,求云梯消防车最高点C距离地面的高度CF.(结果精确到0.1m,参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40.)
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=900,∠BAD=600,对角线AC平分∠BAD,且AB=AC=4,点E、F分别是AC、BC的中点,连接DE,EF,DF,则DF的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
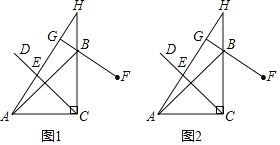
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,E为∠ACB平分线CD上一动点(不与点C重合),点E关于直线BC的对称点为F,连接AE并延长交CB延长线于点H,连接FB并延长交直线AH于点G.
(1)求证:AE=BF.
(2)用等式表示线段FG,EG与CE的数量关系,并证明.
(3)连接GC,用等式表示线段GE,GC与GF的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF

(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图:
(1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C;
(2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
根据以上作图过程及所作图形,下列结论中错误的是( )

A.∠ABD=90°B.CA=CB=CDC.sinA=![]() D.cosD=
D.cosD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上一点(0<AD<![]() AB).过点B作BE⊥CD,垂足为E.将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF.设∠BCE的度数为α.
AB).过点B作BE⊥CD,垂足为E.将线段CE绕点C逆时针旋转90°,得到线段CF,连接AF,EF.设∠BCE的度数为α.
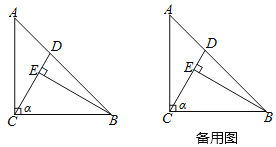
(1)①依题意补全图形.
②若α=60°,则∠CAF=_____°;![]() =_____;
=_____;
(2)用含α的式子表示EF与AB之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
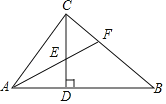
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②a+b+c≥ax2+bx+c;③若M(n2+1,y1),N(n2+2,y2)为函数图象上的两点,则y1>y2.④若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值2个.有其中正确的有( )个.
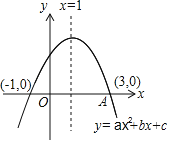
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丹要测量灯塔市葛西河生态公园里被湖水隔开的两个凉亭![]() 和
和![]() 之间的距离,她在
之间的距离,她在![]() 处测得凉亭
处测得凉亭![]() 在
在![]() 的南偏东
的南偏东![]() 方向,她从
方向,她从![]() 处出发向南偏东
处出发向南偏东![]() 方向走了
方向走了![]() 米到达
米到达![]() 处,测得凉亭
处,测得凉亭![]() 在
在![]() 的东北方向.
的东北方向.

(1)求![]() 的度数;
的度数;
(2)求两个凉亭![]() 和
和![]() 之间的距离(结果保留根号).
之间的距离(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com