
已知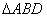 和
和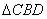 关于直线
关于直线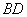 对称(点
对称(点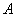 的对称点是点
的对称点是点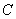 ),点
),点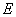 、
、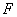 分别是线段
分别是线段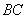 和线段
和线段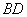 上的点,且点
上的点,且点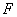 在线段
在线段 的垂直平分线上,联结
的垂直平分线上,联结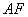 、
、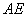 ,
,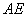 交
交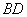 于点
于点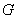 .
.
(1)如图(1),求证: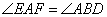 ;
;
(2)如图(2),当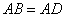 时,
时,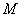 是线段
是线段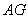 上一点,联结
上一点,联结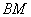 、
、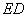 、
、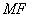 ,
,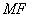 的延
的延 长线交
长线交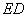 于点
于点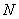 ,
,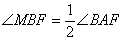 ,
,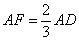 ,试探究线段
,试探究线段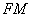 和
和 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.

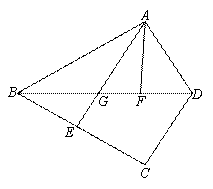
图(1) 图(2)
(1)证明:如图1 连接FE、FC
 ∵点F在线段EC的垂直平分线上,
∵点F在线段EC的垂直平分线上,
∴ FE=FC ∴∠l=∠2
∵△ABD和△CBD关于直线BD对称.
∴AB=CB ,∠4=∠3,又BF=BF
∴△ABF≌△CBF, ∴∠BAF=∠2,FA=FC
∴FE=FA,∠1=∠BAF.∴∠5=∠6,
∵ ∠l+∠BEF=1800,∴∠BAF+∠BEF=1800
∵∠BAF+∠BEF+∠AFE+∠ABE=3600
∴∠AFE+∠ABE=1800
又∵∠AFE+∠5+∠6=1800 ,
∴∠5+∠6=∠3+∠4
∴∠5=∠4,即∠EAF=∠ABD
(2)解:FM= FN
FN
 证明:如图2,由(1)可知∠EAF=∠ABD,
证明:如图2,由(1)可知∠EAF=∠ABD,
又∵∠AFB=∠GFA ∴△AFG∽△BFA
∴∠AGF=∠BAF
又∵∠MBF= ∠B
∠B AF,∴∠MBF=
AF,∴∠MBF= ∠AGF
∠AGF
又∵∠AGF=∠MBG+∠BMG∴∠MBG=∠BMG
∴BG=MG
∵AB=AD ∴∠ADB=∠ABD=∠EAF
又∵∠FGA=∠AGD.∴△AGF∽△DGA.

∵AF=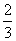 AD
AD
 图2
图2
设GF=2a,则AG=3a,
∴GD= a,∴FD=DG-GF=
a,∴FD=DG-GF= =
=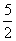 a
a
∵∠CBD=∠ABD ,∠ABD=∠ADB,∴∠CBD=∠ADB.
∴ .∴
.∴
 ,设EG=2k,则MG=BG=3k
,设EG=2k,则MG=BG=3k
过点F作FQ∥ED交AE于Q,


∴GQ=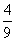 EG=
EG= .∴QE=
.∴QE= , MQ=MG+GQ=3k+
, MQ=MG+GQ=3k+ =
=
∵FQ∥ED, .∴FM=
.∴FM= FN
FN


科目:初中数学 来源: 题型:
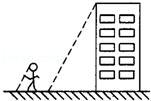
如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和10米.已知小华的身高为1.6米,那么他所住楼房的高度为_______.
A.8 米 B.16米 C.32
米 B.16米 C.32 米 D.48米
米 D.48米

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若 ,求
,求 的值.
的值.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
一个口袋里放有三枚除颜色外都相同的棋子,其中有两枚是白色的,一枚是红色的.从中随机摸出一 枚记下颜色,放回口袋搅匀,再从中随机摸出一枚记下颜色,两次摸出棋子颜色不同的概率是_______.
枚记下颜色,放回口袋搅匀,再从中随机摸出一枚记下颜色,两次摸出棋子颜色不同的概率是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
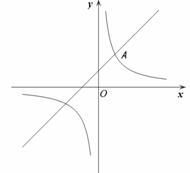
如图,一次函数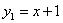 的图象与反比例函数
的图象与反比例函数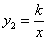 (
(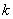 为常数,且
为常数,且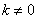 )的图象都经过点
)的图象都经过点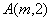 .
.
(1)求点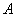 的坐标及反比例函数的解析式;
的坐标及反比例函数的解析式;
(2)观察图象,当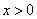 时,直接写出
时,直接写出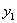 与
与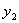 的大小关系.
的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com