



科目:初中数学 来源:不详 题型:单选题
| A.一组对边平行,另一组对边相等 | B.一组对边平行且相等 |
| C.两组对边分别平行 | D.对角线互相平分 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ”型甬道,甬道宽度相等,甬道面积是整个梯形面积的
”型甬道,甬道宽度相等,甬道面积是整个梯形面积的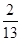 .设甬道的宽为
.设甬道的宽为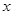 米.
米.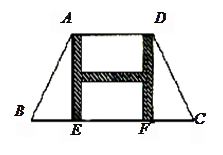
 的周长;
的周长; 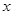 的式子表示甬道的总长;
的式子表示甬道的总长;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
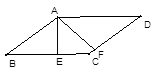
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,
, ,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则
,圆A与圆C交于B、D两点),连结AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则 应满足什么条件?
应满足什么条件? ,求四边形ABCD的面积.
,求四边形ABCD的面积.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的矩形,接着把其中一个面积为
的矩形,接着把其中一个面积为 的矩形等分成两个面积为
的矩形等分成两个面积为 的矩形,再把其中一个面积为
的矩形,再把其中一个面积为 的矩形等分成两个面积为
的矩形等分成两个面积为 的矩形,如此进行下去,试利用图形所揭示的规律计算:
的矩形,如此进行下去,试利用图形所揭示的规律计算:
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com