
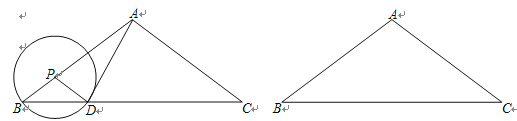
【题目】如图,已知在△ABC中,AB=AC=5,cosB=![]() ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
【答案】(1)12(2)y= ![]() (0<x<5)(3)
(0<x<5)(3)![]() 或
或![]()
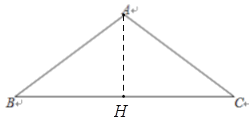
【解析】试题分析:(1)过点A作AH⊥BC于点H ,根据cosB=![]() 求得BH的长,从而根据已知可求得AH的长,BC的长,再利用三角形的面积公式即可得;
求得BH的长,从而根据已知可求得AH的长,BC的长,再利用三角形的面积公式即可得;
(2)先证明△BPD∽△BAC,得到![]() =
=![]() ,再根据
,再根据![]() ,代入相关的量即可得;
,代入相关的量即可得;
(3)分情况进行讨论即可得.
试题解析:(1)过点A作AH⊥BC于点H ,则∠AHB=90°,∴cosB=![]() ,
,
∵cosB=![]() ,AB=5,∴BH=4,∴AH=3,
,AB=5,∴BH=4,∴AH=3,
∵AB=AC,∴BC=2BH=8,
∴S△ABC=![]() ×8×3=12
×8×3=12
(2)∵PB=PD,∴∠B=∠PDB,
∵AB=AC,∴∠B=∠C,∴∠C=∠PDB,
∴△BPD∽△BAC,
∴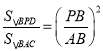 ,
,
即![]() ,
,
解得![]() =
=![]() ,
,
∴![]() ,
,
∴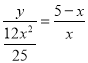 ,
,
解得y= ![]() (0<x<5);
(0<x<5);
(3)∠APD<90°,
过C作CE⊥AB交BA延长线于E,可得cos∠CAE=![]() ,
,
①当∠ADP=90°时,
cos∠APD=cos∠CAE=![]() ,
,
即![]() ,
,
解得x=![]() ;
;
②当∠PAD=90°时,
![]() ,
,
解得x=![]() ,
,
综上所述,PB=![]() 或
或![]() .
.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
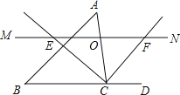
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,|5(2)|表示5与2之差的绝对值,实际上也可理解为5与2两数在数轴上所对应的两点之间的距离,试探索:
(1)求|5(2)|=___.
(2)若|x2|=5,则x=___
(3)同理|x+5|+|x2|表示数轴上有理数x所对应的点到5和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得|x+5|+|x2|=7,这样的整数是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人沿相同的路线由![]() 地到
地到![]() 地匀速前进,
地匀速前进,![]() ,
,![]() 两地间的路程为
两地间的路程为![]() .他们前进的路程为
.他们前进的路程为![]() ,甲出发后的时间为
,甲出发后的时间为![]() ,甲,乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法不正确的是( )
,甲,乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法不正确的是( )
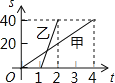
A.甲的速度是![]() B.乙出发
B.乙出发![]() 后与甲相遇
后与甲相遇
C.乙的速度是![]() D.甲比乙晚到
D.甲比乙晚到![]() 地
地![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ADBC,BC,垂足分别为D、F,23180,试说明:GDCB,请补充说明过程,并在括号内填上相应的理由。
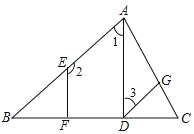
解:ADBC,EFBC(已知)
ADBEFB90( ① ),
EF//AD( ② ),
③ 2180( ④ ),
又23180(已知),
13( ⑤ ),
AB// ⑥ ( ⑦ ),
∴∠GDC=∠B( ⑧ )
查看答案和解析>>
科目:初中数学 来源: 题型:
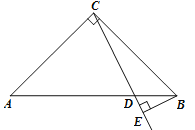
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转![]() ,得到线段CF,连结EF.设∠BCE度数为
,得到线段CF,连结EF.设∠BCE度数为![]() .
.
(1)①补全图形;
②试用含![]() 的代数式表示∠CDA.
的代数式表示∠CDA.
(2)若![]() ,求
,求![]() 的大小.
的大小.
(3)直接写出线段AB、BE、CF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有三个分别标记为“-1”、“2”、“ -3”的球,这三个球除了标记不同外,其余均相同.搅匀后,从中摸出一个球,记录球上的标记为![]() 后,放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记为
后,放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记为![]() ,最终结果记录为
,最终结果记录为![]() .
.
(1)请用“画树状图”或“列表”等方法写出上述实验中所记录球上标记的所有可能的结果;
(2)若将记录结果![]() 看成平面直角坐标系中的一点,求
看成平面直角坐标系中的一点,求![]() 是第二象限内的点的概率.
是第二象限内的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:
年人均收入 | 3 500 | 3 700 | 3 800 | 3 900 | 4 500 |
村庄个数 | 1 | 1 | 3 | 3 | 1 |
该乡去年各村庄年人均收入的中位数是( )
A.3 700元B.3 800元C.3 850元D.3 900元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com