
【题目】已知:如图,在四边形ABCD中,AD∥BC,连接对角线AC.
(1)在边AD上确定一点E,使EA=EC;在边BC上确定一点F,使FA=FC;(尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,连接AF,CE.求证:四边形AFCE是菱形.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低 ( )

A. 星期二B. 星期四C. 星期六D. 星期五
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
【1】如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
【1】在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
【1】如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD=![]() ,求BC的长.
,求BC的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的对应点如图所示
![]()
(1) 填空:(填“<”、“>”或“=”)
a_________0;b_________0;|a+b|_________|a|+|b|
(2) 用“<”将a、b、-b、![]() 、0连接起来
、0连接起来
(3) 化简:|a+b|-|b+1|-|a-1|=______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有1个白球、3个红球和6个黄球,这些球除颜色外都相同,将球摇匀.
(1) 从中任意摸出1个球,摸到 球的可能性大.
(2) 若现拿红球和黄球共7个球放入袋中,你认为怎样放才能让摸到红球和黄球的可能性相同?(直接回答,无需解题过程)
(3) 若从中摸出5个球,其中有![]() 个黄球,当
个黄球,当![]() = 时,“摸到白球”是必然事件?
= 时,“摸到白球”是必然事件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宽与长的比是 ![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC,的平分线,交AD的延长线于点H,作HG⊥BC,交I3C的延长线于点G,则下列矩形是黄金矩形的是( )
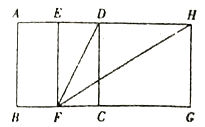
A. 矩形ABFE B. 矩形EFCD C. 矩形EFGH D. 矩形DCGH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交与
的图像交与![]() ,
,![]() 两点,过点A作
两点,过点A作![]() 轴于点C,过点B作
轴于点C,过点B作![]() 轴于点D,连接AO,
轴于点D,连接AO,![]() 得出以下结论:
得出以下结论:
①点A和点B关于直线![]() 对称;
对称;
②当![]() 时,
时,![]() ;
;
③![]() ;
;
④当![]() 时,
时,![]() ,
,![]() 都随x的增大而增大.
都随x的增大而增大.
其中正确的是![]()
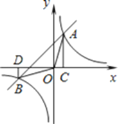
A.①②③B.②③C.①③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com