
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

【答案】(1)y=![]() x+2;(2)﹣6<x<0或x>2;(3)(﹣2,0)或(﹣6,0)
x+2;(2)﹣6<x<0或x>2;(3)(﹣2,0)或(﹣6,0)
【解析】分析:(1)把点A、B的坐标分别代入反比例函数解析式中,求出m、n的值,得到点A、B的坐标,再将点A、B的坐标分别代入一次函数解析式中即可确定出一次函数解析式;
(2)结合图象,根据两函数的交点横坐标,找出一次函数图象在反比例图象上方时x的范围即可;
(3)先求出△BOC的面积,再根据S△ACP=![]() S△BOC求出CP的长,进而得到点P的坐标.
S△BOC求出CP的长,进而得到点P的坐标.
详解:(1)将A(m,3)代入反比例解析式得:m=2,则A(2,3),
将B(-6,n)代入反比例解析式得:n=-1,则B(-6,-1),
将A与B的坐标代入y=kx+b得:![]() ,
,
解得:![]() ,
,
则一次函数解析式为y=![]() x+2;
x+2;
(2)由图象得:![]() x+2>
x+2>![]() 的x的取值范围是:-6<x<0或x>2;
的x的取值范围是:-6<x<0或x>2;
(3)∵y=![]() x+2中,y=0时,
x+2中,y=0时,![]() x+2=0,
x+2=0,
解得x=-4,则C(-4,0),OC=4
∴△BOC的面积=![]() ×4×1=2,
×4×1=2,
∴S△ACP=![]() S△BOC=
S△BOC=![]() ×2=3.
×2=3.
∵S△ACP=![]() CP×3=
CP×3=![]() CP,
CP,
∴![]() CP=3,
CP=3,
∴CP=2,
∵C(-4,0),
∴点P的坐标为(-2,0)或(-6,0).


科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
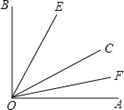
(1)若∠AOB=90°,∠AOC=30°,求∠EOF的度数;
(2)若∠AOB=![]() ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);
(3)若将条件中“OE平分∠BOC,OF平分∠AOC.平分”改为“∠EOB=![]() ∠COB,∠COF=
∠COB,∠COF=![]() ∠COA”,且∠AOB=
∠COA”,且∠AOB=![]() ,求∠EOF的度数(写出求解过程).
,求∠EOF的度数(写出求解过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
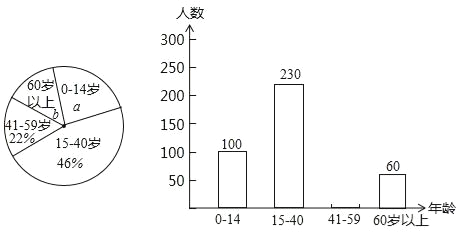
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,点O为坐标原点,点A在x轴正半轴上,点C在第一象限,且∠COA=60°,以OA、OC为邻边作菱形OABC,且菱形OABC的面积为![]() .
.
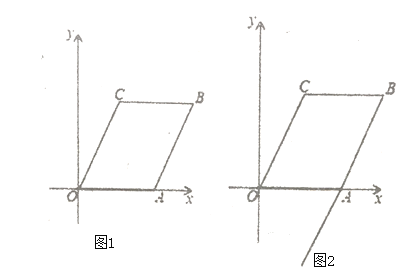
(1)求B. C两点的坐标;
(2)动点P从C点出发沿射线CB匀速运动,同时动点Q从A点出发沿射线BA的方向匀速运动,P、Q两点的运动速度均为2个单位/秒,连接PQ和AC,PQ和AC所在直线交于点D,点E为线段BQ的中点,连接DE,设动点P、Q的运动时间为t,请将△DQE的面积S用含t的式子表示,并直接写出t的取值范围;
(3)在(2)的条件下,过点Q作QF⊥y轴于点F,当t为何值时,以P、B.、F.、Q为顶点的四边形为平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
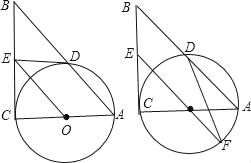
【题目】【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料![]() :我们知道,如果一个三角形的三边长固定,那么这个三角形就固定。若给出任意一个三角形的三边长,你能求出它的面积吗?设一个三角形的三边长分别为
:我们知道,如果一个三角形的三边长固定,那么这个三角形就固定。若给出任意一个三角形的三边长,你能求出它的面积吗?设一个三角形的三边长分别为![]() ,
,![]() ,
,![]() ,我们把它的面积记为
,我们把它的面积记为![]() ,古希腊的几何学家海伦(Hcron,约公元50年),在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个通过三角形的三边长来求面积的海伦公式。我们可以把海伦公式变形为:
,古希腊的几何学家海伦(Hcron,约公元50年),在数学史上以解决几何测量问题而闻名,在他的著作《度量》一书中,给出了一个通过三角形的三边长来求面积的海伦公式。我们可以把海伦公式变形为:![]() (其中
(其中![]() )
)
材料2:把形如![]() 的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即
的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即![]() .配方法是中学数学的重要方法,用配方法可求最最大(小)值.
.配方法是中学数学的重要方法,用配方法可求最最大(小)值.
例如:求![]() 的最小值.
的最小值.
![]()
![]()
![]()
![]()
![]()
当![]() 时,
时,![]() ,此时
,此时![]() 取得最小值
取得最小值![]() ,
,
请你运用材料提供的方法,解答以下问题:
(1)若三角形的三边长分别为![]() ,
,![]() ,
,![]() ,求该三角形的面积;
,求该三角形的面积;
(2)小新手里有一根长![]() 米的铁丝,他想用这根铁丝制作一个三角形模型,要求该三角形的一边长为
米的铁丝,他想用这根铁丝制作一个三角形模型,要求该三角形的一边长为![]() 米且面积最大,请你帮助他计算出这个三角形另两边的边长,并说明理由.
米且面积最大,请你帮助他计算出这个三角形另两边的边长,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
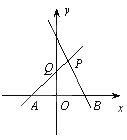
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古就是中国的!2017年5月18日,中国海警2305,2308,2166,33115舰船队在中国的钓鱼岛领海内巡航,如图,我军以30km/h的速度在钓鱼岛A附近进行合法巡逻,当巡逻舰行驶到B处时,战士发现A在他的东北方向,巡逻舰继续向北航行40分钟后到达点C,发现A在他的东偏北15°方向,求此时巡逻舰与钓鱼岛的距离(![]() ≈1.414,结果精确到0.01)
≈1.414,结果精确到0.01)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com