
分析 (1)由利润y=(销售单价-成本单价)×件数,及销售单价均不低于2600元,按10<x≤50,x>50两种情况列出函数关系式;
(2)根据(2)中函数关系式列出方程,解之可得x的值,根据题意取舍后可得答案;
(3)将10≤x≤50时的函数解析式配方成顶点式,根据二次函数性质可得.
解答 解:(1)当一次购买这种产品x(x≥10)件时,销售单价为3000-10(x-10),
由题意可知,3000-10(x-10)≥2600,
解得:x≤50,
∴当10≤x≤50时,y=[3000-10(x-10)-2400]x,即y=-10x2+700x;
当x>50时,y=(2600-2400)x=200x;
(2)当0≤x<10时,由600x=12000可得x=20>10,舍去;
当10≤x≤50时,-10x2+700x=12000,
解得:x=30或x=40,
当x>50时,200x=12000,
解得:x=60,
∵客户购买产品的件数应尽可能少,
∴x=30,
答:商场销售了30件产品时,商场所获的利润为12000元;
(3)∵当10≤x≤50时,y=-10x2+700x=-10(x-35)2+12250,
∴当35<x≤50时,y随x的增大而减小,
即客户一次购买产品的数量x满足的35<x≤50时,会出现随着一次购买的数量的增多,商场所获的利润反而减少这一情况,
故答案为:35<x≤50.
点评 本题主要考查二次函数的应用和一元二次方程的应用能力,理解题意得出相等关系,并据此列出函数解析式及方程是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
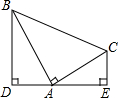 如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,
如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -2 | C. | 3 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com