
分析 (1)先证明△MBN≌△DCN,得NB=NC,再证明∠NCE=∠NEC,由等角对等边可知NC=NE,所以NB=NC=NE;
(2)结论仍然成立,作辅助线,构建全等三角形,先根据直角三角形斜边上的中线得出AN=DN,证明△ABN≌△DCN,得NB=NC,再根据角的关系求出∠NCE=∠DCN+45°,∠CEN=∠EGD+45°,所以∠NCE=∠CEN,则NC=NE,结论成立;
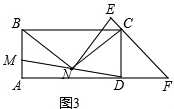
(3)NB=NC=NE,如图3,延长EN交AD于G,连接AN,同理得出NB=NC,再根据∠NEF=∠ECN,得NC=NE,所以NB=NC=NE.
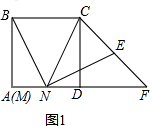
解答 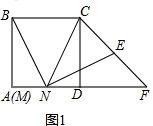 解:(1)如图1,在正方形ABCD 中,
解:(1)如图1,在正方形ABCD 中,
∵AB=CD,∠A=∠ADC,MN=DN,
∴△MBN≌△DCN,
∴NB=NC,
∵NE⊥BN
∴∠BNE=90°
∴∠BNA+∠ENF=90°,
∵∠ABN+∠ANB=90°,
∴∠ABN=∠ENF,
∵∠ABN=∠NCD,
∴∠NCD=∠ENF,
∵CD=DF,∠CDF=90°,
∴∠F=∠DCF=45°,
∵∠NCE=∠DCN+∠DCF=∠DCN+45°,∠CEN=∠ENF+∠F=∠ENF+45°,
∴∠NCE=∠NEC,
∴NC=NE,
∴NB=NC=NE;
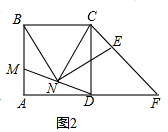
(2)成立,如图2,延长EN交AD于G,连接AN,
在Rt△ADM中,
∵N是MD的中点,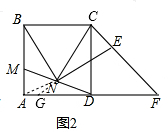
∴AN=DN,
∴∠NAD=∠NDA,
∴∠BAN=∠MDC,
∵AB=CD,
∴△ABN≌△DCN,
∴NB=NC,
∵NE⊥BN,
∴∠ABN+∠AGN=180°,
∵∠EGD+∠AGN=180°,
∴∠ABN=∠EGD,
∵∠ABN=∠DCN,
∴∠EGD=∠DCN,
∵CD=DF,∠CDF=90°,
∴∠F=∠DCF=45°
∵∠NCE=∠DCN+∠DCF=∠DCN+45°,∠CEN=∠EGD+∠F=∠EGD+45°,
∴∠NCE=∠CEN,
∴NC=NE,
∴NB=NC=NE;
(3)NB=NC=NE,理由是:
如图3,延长EN交AD于G,连接AN,
同理得AN=DN,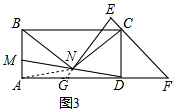
∴∠NAD=∠NDA,
∴∠BAN=∠NDC,
∵四边形ABCD为矩形,
∴AB=CD,
∴△ABN≌△DCN,
∴NB=NC,
∵NE⊥BN,
∴∠ABN+∠AGN=180°,
∵∠EGD+∠AGN=180°,
∴∠ABN=∠EGD,
∵∠ABN=∠DCN,
∴∠EGD=∠DCN,
∵∠F=∠DCF=45°,
在△EGF中,∠NEF=180°-∠EGD-∠F=135°-∠EGD,
∠ECN=180°-∠DCN-∠DCF=135°-∠DCN,
∴∠NEF=∠ECN,
∴NC=NE,
∴NB=NC=NE.
点评 本题是四边形的综合题,考查了正方形、矩形的性质及三角形全等的性质和判定;同时还利用了直角三角形斜边上的中线等于斜边一半证明边相等,从而得出角的关系;本题的三个问题是从特殊到一般,都是先利用全等得出NB=NC,再根据等腰三角形的判定得出NE=NC,从而使问题得以解决.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 125个 | C. | 250个 | D. | 499个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
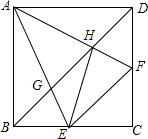 如图,正方形ABCD中,点E,F分别在BC、DC上,∠EAF=45°,AE,AF分别交BD于G,H,下列结论
如图,正方形ABCD中,点E,F分别在BC、DC上,∠EAF=45°,AE,AF分别交BD于G,H,下列结论| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com