
【题目】如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.
(1)求证:△BEC≌△CDB;
(2)若∠A=70°,BE⊥AC,求∠BCD的度数.

【答案】见解析
【解析】试题分析:(1)利用△ABE≌△ACD,得BE=CD,BD=CE,一条公共边,BC=BC,利用SSS证明.
(2)利用(1)结论,可知∠ACD=∠ABE=20°,由内角和180°,可知∠EBC+∠DCB=70°,可得∠BCD的度数.
试题解析:
(1)证明:∵△ABE≌△ACD,
∴AB=AC,AD=AE,BE=CD,
∴BD=CE,
在△BEC与△CDB中,
BD=CE,CD=BE,BC=CB,
∴△BEC≌△CDB.
(2)解:∵AB=AC,∠A=70°,
∴∠ACB=∠ABC=55°,
∵BE⊥AC,
∴∠BEC=∠AEB=90°,
∴∠ABE=∠ACD=20°,
∴∠BCD=35°.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.四个内角对应相等的两个四边形一定相似
B.四条边对应成比例的两个四边形一定相似
C.一个顶角对应相等的两个等腰三角形相似
D.两条边对应成比例且有一个内角相等的两个三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( ) 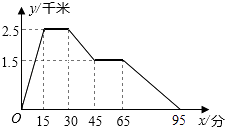
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米
D.张强从早餐店回家的平均速度是3千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
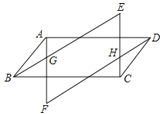
【题目】如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE与G点,交DF与F点,CE交DF于H点、交BE于E点.求证:△EBC≌△FDA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小头爸爸”为了检查“大头儿子”对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.“大头儿子”稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧. 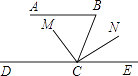
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以每秒2cm的速度沿图甲的边框按BCDEFA的路径移动,相应的三角形ABP的面积S(cm2)与时间t(秒)之间的关系用图乙中的图象表示,若AB=6cm,试回答下列问题: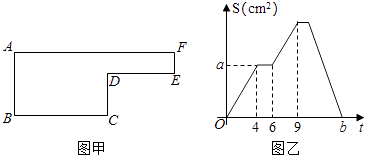
(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com