练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．把抛物线y=-x2向左平移2个单位，再向下平移3个单位，所得抛物线的函数关系式为y=-（x+2）2-3．

    分析 先根据顶点式得到抛物线y=-x2的顶点坐标为（0，0），再利用点平移的规律得到点（0，0）平移后所得对应点的坐标为（-2，-3），然后根据顶点式写出新抛物线解析式．

    解答 解：抛物线y=-x2的顶点坐标为（0，0），把点（0，0）向左平移2个单位，再向下平移3个单位所得对应点的坐标为（-2，-3），所以所得抛物线的函数关系式为y=-（x+2）2-3．
    故答案为y=-（x+2）2-3．

    点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．如图的几何体中，其主视图为三角形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

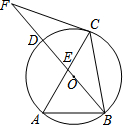    7．如图，△ABC内接于⊙O，∠A=60°，点F是直径BD的延长线上一点，且CF=CB．
    （1）求∠CBF的度数；
    （2）判断直线CF与⊙O的位置关系，并证明；
    （3）若AB=3，BC=2$\sqrt{3}$，tan∠AEB=3，求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，把一块含有30°的三角板的两个顶点放在一长方形纸片的对边上．如果∠1=20°，那么∠2的度数是40度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知方程组$\left\{\begin{array}{l}{2x-y=1}\\{2x+y=m}\end{array}\right.$的解$\left\{\begin{array}{l}{x≤1}\\{y＞\frac{1}{2}}\end{array}\right.$．求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知方程组$\left\{\begin{array}{l}{mx+y=2}\\{x-my=-1}\end{array}\right.$的解x，y的值小于零，试求$\frac{|2m-1|}{2m-1}$-$\frac{|m+2|}{m+2}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．当a=1时，代数式2a-3的值为-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

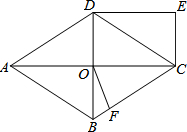    5．如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．
    （1）求证：四边形OCED为矩形；
    （2）在BC上截取CF=CO，连接OF，若AC=16，BD=12，求四边形OFCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，为测量某楼AB的高度，工作人员在点D处高1.8m的测角仪CD测得楼顶端A的仰角为30°，向前走40m到点E，又测得点A的仰角为60°，求楼AB的高度．（最后结果取近似值，保留两位小数，参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）

    查看答案和解析>>

    同步练习册答案