
【题目】如图,在△ABC中,点D在边AC上,DB=BC=AD,E是CD的中点,F是AB的中点,
(1)求证:EF=![]() AB.
AB.
(2) 当∠C=60 时, BC 、AB 与AC满足怎么样的关系?(直接写出答案,不必说明理由)

【答案】(1)证明见解析;(2)BC2+AB2=AC2.
【解析】试题分析:(1)连接BE,根据等腰三角形三线合一的性质可得BE⊥AC,再根据直角三角形斜边上的中线等于斜边的一半证明;(2)根据题意得出△BCD是等边三角形,得∠CBD=∠CDB=60°,再根据BD=AD,得出∠A=∠DBA=30°,再得出△ABC是直角三角形,从而得证.
解: (1)证明:连接BE,
∵BC=BD,E是CD的中点,
∴BE⊥AC,
又∵F是AB的中点,
∴EF=![]() AB.
AB.
(2)∵BC=BD,∠C=60 ,
∴△BCD是等边三角形,
∴∠CBD=∠CDB=60°,
∵BD=AD,
∴∠A=∠DBA=![]() ∠CDB=30°,
∠CDB=30°,
∴∠ABC=∠CBD+∠DBA=60°+30°=90°,
∴BC2+AB2=AC2.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如表所示:
用电量(度) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
则这20户家庭该月用电量的众数和中位数分别是( )
A.180,160
B.160,180
C.160,160
D.180,180
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是边长为4的正方形,点P从点O沿边OA向点A运动,每秒运动1个单位.连结CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点E作EF∥OA,交OB于点F,连结FD、BE,设点P运动的时间为![]()
![]() .
.
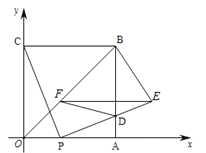
(1)点E的坐标为 (用含![]() 的代数式表示);
的代数式表示);
(2)试判断线段EF的长度是否随点P的运动变化而改变?并说明理由;
(3)当![]() 为何值时,四边形BEDF的面积为
为何值时,四边形BEDF的面积为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com