
 在△ABC中,∠C=90°,△ABC的两锐角平分线AD、BE交于点O.
在△ABC中,∠C=90°,△ABC的两锐角平分线AD、BE交于点O. 解:(1)∵直角△ABC的两锐角平分线AD、BE交于点O,
解:(1)∵直角△ABC的两锐角平分线AD、BE交于点O,| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| A、35元 | B、40元 |
| C、45元 | D、48元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
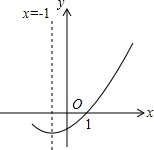 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0②b=2a;③当-3<x<1时,ax2+bx+c<0;④a-b<m(am+b)(m≠-1).其中正确的命题有( )
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0②b=2a;③当-3<x<1时,ax2+bx+c<0;④a-b<m(am+b)(m≠-1).其中正确的命题有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1条、4条、8条或10条 |
| B、1条、5条、9条或10条 |
| C、1条、5条、8条或10条 |
| D、1条或10条 |
查看答案和解析>>
科目:初中数学 来源: 题型:
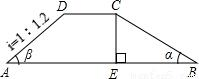 如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.
如图,水坝的横截面积是梯形ABCD,迎水坡BC的坡角α为30°,背水坡AD的坡度i,即(tanβ)为1:1.2,坝顶宽DC=2.5m,坝高4.5m.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com