
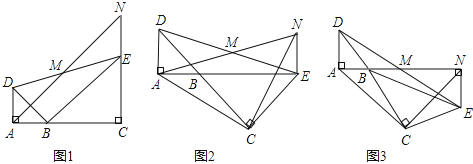
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)△ACN仍为等腰直角三角形,证明见解析.
【解析】
试题(1)由EN∥AD和点M为DE的中点可以证到△ADM≌△NEM,从而证到M为AN的中点.
(2)易证AB=DA=NE,∠ABC=∠NEC=135°,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
(3)同(2)中的解题可得AB=DA=NE,∠ABC=∠NEC=180°﹣∠CBN,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
试题解析:解:(1)证明:如图1,
∵EN∥AD,∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为DE的中点,∴DM=EM.
在△ADM和△NEM中,∵ ,∴△ADM≌△NEM(AAS).
,∴△ADM≌△NEM(AAS).
∴AM=MN.∴M为AN的中点.
(2)证明:如图2,
∵△BAD和△BCE均为等腰直角三角形,∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD∥NE,∴∠DAE+∠NEA=180°.
∵∠DAE=90°,∴∠NEA=90°.∴∠NEC=135°.
∵A,B,E三点在同一直线上,∴∠ABC=180°﹣∠CBE=135°.∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),∴AD=NE.
∵AD=AB,∴AB=NE.
在△ABC和△NEC中,∵ ,∴△ABC≌△NEC(SAS).
,∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
(3)△ACN仍为等腰直角三角形.证明如下:
如图3,此时A、B、N三点在同一条直线上.
∵AD∥EN,∠DAB=90°,∴∠ENA=∠DAN=90°.
∵∠BCE=90°,∴∠CBN+∠CEN=360°﹣90°﹣90°=180°.
∵A、B、N三点在同一条直线上,∴∠ABC+∠CBN=180°.∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),∴AD=NE.
∵AD=AB,∴AB=NE.
在△ABC和△NEC中,∵ ,∴△ABC≌△NEC(SAS).
,∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正△ABC中,D,E分别在AC,AB上,且 ![]() ,AE=BE,则有( )
,AE=BE,则有( )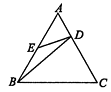
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 ![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,![]() ),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板直角顶点重合于点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)如图(1),若![]() ,求证:
,求证:![]() ;
;
(2)如图(2),若![]() ,
,![]() ,则
,则![]() 度;
度;
(3)如图(3),在(1)的条件下,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
.
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
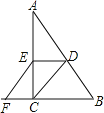
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在四边形ABCD中,点E、点F分别为AD、BC的中点,连接EF.
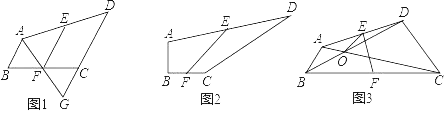
(1)如图1,AB∥CD,连接AF并延长交DC的延长线于点G,则AB、CD、EF之间的数量关系为 ;
(2)如图2,∠B=90°,∠C=150°,求AB、CD、EF之间的数量关系?
(3)如图3,∠ABC=∠BCD=45°,连接AC、BD交于点O,连接OE,若AB=![]() ,CD=2
,CD=2![]() ,BC=6,则OE= .
,BC=6,则OE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com