
 如图,AD,BE,CF是△ABC的高,K,M,N分别为△AEF,△BFD,△CDE的垂心,求证:△DEF≌△KMN.
如图,AD,BE,CF是△ABC的高,K,M,N分别为△AEF,△BFD,△CDE的垂心,求证:△DEF≌△KMN. 分析 根据垂心的条件,得出OD与FM同时垂直于BC,OF与DM同时垂直于AB,进而得出DMFO是平行四边形,同理得出OFEK,OEND也是平行四边形,进一步可得KEDM,FKND,FMNE也是平行四边形,得出要证明的两个三角形三边对应相等,结论显然.
解答 证明:如图: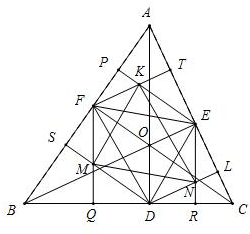
∵OD⊥BC,FM⊥BC,
∴OD∥FM,
∵OF⊥AB,DM⊥AB,
∴OF∥DM,
∵DMFO是平行四边形,
同理OFKE,ODNE均为平行四边形,
∴MD∥KE,MD=KE,
∴MDEK也是平行四边形,
∴DE=MK,
同理DF=KN,EF=MN
∴△DEF≌△KMN(SSS).
点评 本题主要考查垂心的定义和性质、平行四边形的判定及性质、全等三角形的判定及性质.利用垂直得出DMFO,OFKE,ODNE均为平行四边形是关键.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
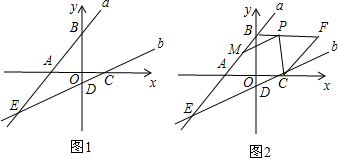
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于点C,与x轴相交于点A、B,点B的坐标为(-1,0),点C的坐标为(0,-1).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于点C,与x轴相交于点A、B,点B的坐标为(-1,0),点C的坐标为(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
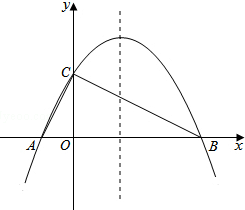 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com