
����Ŀ����ͼ������������������A��B��C������������⣺
![]()
(1)����B�����ƶ�������λ���ȵ���D���������ϱ�ʾ����D��
(2)���������ҵ���E��ʹ��EΪBA���е㣨E��A��C����ľ�����ȣ������������ϱ����E��ʾ���������CE�ij���
(3)OΪԭ�㣬ȡOC���е�M����OC��Ϊ���Σ���Ϊ��һ�β�����ȡ������OM��CM���е�ֱ�Ϊ��N1��N2����OC��Ϊ4�Σ���Ϊ�ڶ��β�������ȡ�����ε��е㽫OC��Ϊ8�Σ���Ϊ�����β����������β�����OC֮�乲�ж��ٸ��㣿�����Щ������ʾ�����ĺͣ�
���𰸡���1����ͼ��ʾ����������2����ͼ��ʾ����E��ʾ����Ϊ����3.5��CE=4������3.5��=7.5����3��OC֮�乲��65���㣻��Щ������ʾ�����ĺ�Ϊ130��
��������
��1�����������ϵĵ��ƶ�ʱ�Ĵ�С�仯���ɣ���������Ҽ������ɵõ����ۣ�
��2������������ʽ���㼴�ɣ�
��3����������õ�������2��ָ������+1���ݴ˼��㼴�ɣ�
��1����ͼ��ʾ��
![]()
��2����ͼ��ʾ����E��ʾ����Ϊ����3.5��
�ߵ�C��ʾ����Ϊ��4��
��CE=4������3.5��=7.5��
��3���ߵ�һ�β�������3=��21+1�����㣬
�ڶ��β�������5=��22+1�����㣬
�����β�������9=��23+1�����㣬
������β�����OC֮�乲�У�26+1��=65���㣻
��65�����ȥ0��64������
����Щ������ʾ�����ĺ�=4����![]() ��=130��
��=130��


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ཫ���С���ѧ֪ʶ��������������С������Ʒ��������ͼ��С����ؽ�Ʒʱ���ĶԻ��龳��

������������Ϣ��������⣺
(1)�Լ������ֱʼDZ������˶��ٱ���
(2)������ͣ�С��Ϊʲô�������һ�68Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
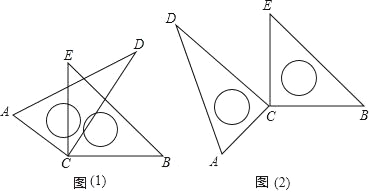
����Ŀ����ѧ����ϣ�С��ͬѧ��Ū���Լ��չ����һ�����ǰ壬������ֱ�����ǰ��ֱ�Ƕ���C������һ��Ȼ��ת�����ǰ壬��ת�������У������������⣺
��1����ͼ��1��������DCE=30��ʱ����ACB+��DCE=�� ��������DCEΪ�������ʱ���㻹�������ACB����DCE��������ϵ�����ܣ�������������ܣ���˵�����ɣ�
��2����ת����ͼ��2�����ʱ����ACB����DCE��������������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�A��ʾ��������Ϊ��6����B��ʾ��������Ϊ6����P�ӵ�A������ÿ��4����λ���ȵ��ٶ�����������A��B�˶�������P�����B���������أ���Ȼ��ÿ��4����λ���ȵ��ٶ��˶�����Aֹͣ�˶������˶�ʱ��Ϊt����λ���룩��
��1����t��1ʱ��P��ʾ����������
��2�����P���B�غ�ʱ��tֵ��
��3���ڵ�P�������ɵ�A����B�ٻص���A���˶������У����P���A�ľ��루�ú�t�Ĵ���ʽ��ʾ����
��4������P��ʾ����������ԭ��ľ�����2����λ����ʱ���������������������tֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ҿ��̳��ƻ�����ij�ֲ��������ν������ۣ��й���Ϣ�����
ԭ���ۣ�Ԫ/�ţ� | ���ۼۣ�Ԫ/�ţ� | �����ۼۣ�Ԫ/�ף� | |
���� | a | 270 | 500Ԫ |
���� | a��110 | 70 |
��֪��600Ԫ�����IJ�����������160Ԫ�����IJ���������ͬ��
��1�������a��ֵ��
��2�������̳��������ε������Dz���������5������20�ţ��Ҳ����Ͳ��ε�������������200�ţ����̳��ƻ���һ��IJ������ף�һ�Ų��������Ų������һ�ף����ۣ�������������������۷�ʽ���ۣ������������������ܻ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����ABCD�Ķ���A������Ϊ��2��0������B������Ϊ��0��1������C�ڵ�һ���ޣ��Խ���BD��x��ƽ�У�ֱ��y=x+3��x�ᡢy��ֱ��ڵ�E��F��������ABCD��x������ƽ��m����λ������D������EOF���ڲ�ʱ�������������εıߣ���m��ȡֵ��Χ�ǣ�������
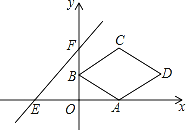
A. 4��m��6 B. 4��m��6 C. 4��m��5 D. 4��m��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����мס�����������,�ֱ�װ�н�ˮ�ܺͳ�ˮ��,�������Ľ�����ˮ�ٶȲ���,�ȴ��������Ľ�ˮ��,2����ʱ�ٴ������Ľ�ˮ��,�ֹ�2���ӹرռ������Ľ�ˮ��,�ٹ�4����ͬʱ�������Ľ�����ˮ��.ֱ��12����ʱ,ͬʱ�ر��������Ľ�����ˮ��.�ر�ˮ�ܵ�ʱ����Բ���.�����е�ˮ��y(��)��������עˮʱ��x(��)֮��Ĺ�ϵ��ͼ��ʾ.
(1)��������Ľ�����ˮ�ٶ�;
(2)�������Ľ�����ˮ�ܶ��رպ�,�Ƿ������������ˮ�����?������,�����ʱ��ʱ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���2730Ԫ����A��B�������ͽ����չ�ƹ�60յ���������չ�ƵĽ��ۡ�������±���ʾ��
�۸�/���� | A�� | B�� |
���ۣ�Ԫ/յ�� | 35 | 65 |
��ۣ�Ԫ/յ�� | 50 | 100 |
��1���������չ�Ƹ���������յ��
��2����A���չ�ư���۵�9�۳��ۣ�Ҫʹ�����չ��ȫ���������̳����810Ԫ��������B���չ��Ӧ����۵ļ��۳��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ�����һ�����֣��ٻش��������⣮
��֪��ƽ��ֱ������ϵ������P1(x1��y1)��P2(x2��y2)����P1��P2��ľ��빫ʽP1P2��![]() ��ͬʱ�����������ڵ�ֱ�����������ϻ�ƽ�����������ֱ��������ʱ�������ľ��빫ʽ�ɼ�Ϊ|x2��x1|��|y2��y1|.
��ͬʱ�����������ڵ�ֱ�����������ϻ�ƽ�����������ֱ��������ʱ�������ľ��빫ʽ�ɼ�Ϊ|x2��x1|��|y2��y1|.
(1)��֪A(2��4)��B(��3����8)������A��B�����ľ��룻
(2)��֪����������ΪA(0��6)��B(��3��2)��C(3��2)�������ж���ABC����״�𣿲�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com