
分析 直接将x的值代入,再利用二次根式的乘法运算法则求出即可.
解答 解:∵x=2-$\sqrt{3}$,
∴(7+4$\sqrt{3}$)x2+($\sqrt{3}$+1)x+$\sqrt{3}$
=(7+4$\sqrt{3}$)(2-$\sqrt{3}$)2+($\sqrt{3}$+1)(2-$\sqrt{3}$)+$\sqrt{3}$
=(7+4$\sqrt{3}$)(7-4$\sqrt{3}$)+2$\sqrt{3}$-3+2-$\sqrt{3}$+$\sqrt{3}$
=49-48+2$\sqrt{3}$-3+2-$\sqrt{3}$+$\sqrt{3}$
=2$\sqrt{3}$.
点评 此题主要考查了二次根式的混合运算,正确掌握二次根式运算法则是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | x轴上方(含x轴) | B. | x轴下方(含x轴) | C. | y轴右方(含y轴) | D. | y轴左方(含y轴) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
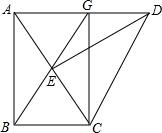 如图,在Rt△ABC中,∠ABC=90°,将Rt△ABC绕点C沿顺时针方向旋转60°得到△DEC,点E在AC上,连接AD,BE,并延长BE交AD于G,连接CG.问:四边形ABCG是什么特殊的四边形?为什么?
如图,在Rt△ABC中,∠ABC=90°,将Rt△ABC绕点C沿顺时针方向旋转60°得到△DEC,点E在AC上,连接AD,BE,并延长BE交AD于G,连接CG.问:四边形ABCG是什么特殊的四边形?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
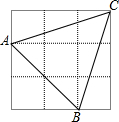 如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题:
如图,小正方形的边长为1,连接小正方形的三个顶点得到△ABC,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com