练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．为了解2016届本科生的就业情况，某网站对该届毕业生的签约情况进行了网络调查，参与网络调查的12000人中，只有9320人已与用人单位签约，在这个网络调查中样本容量是12000．

    分析 总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．

    解答 解：为了解2016届本科生的就业情况，某网站对该届毕业生的签约情况进行了网络调查，参与网络调查的12000人中，只有9320人已与用人单位签约，在这个网络调查中样本容量是12000，
    故答案为：12000．

    点评 考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．直线y=2x+6与x轴的交点坐标为（　　）
    A．（-3，0）B．（3，0）C．（0，6）D．（0，-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

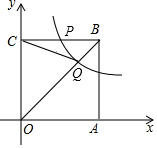    11．如图，平面直角坐标系中，O为坐标原点，正方形ABCO的两边OA、OC分别与x轴、y轴重合，点P是CB的中点，过点P的反比例函数y=$\frac{k}{x}$的图象交对角线OB与点Q，△COQ的面积为2，求k的值为2$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若方程mx+ny=6的两个解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$，则m-n=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．某市为了分析全市9600名初中毕业生的中考数学考试成绩，共抽取15本试卷进行调查，其中每本试卷都是30份，该调查的样本容量是450．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，有种地板样式，如果小球分别在上面自由滚动，设小球在这种地板上最终停留在黑色区域的概率为P1，则P1=$\frac{3}{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，已知菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=2$\sqrt{2}$，BD=4，则菱形ABCD的面积为（　　）
    A．2$\sqrt{2}$B．4$\sqrt{2}$C．8$\sqrt{2}$D．16$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知x、y是实数，且$\root{3}{z}$=2，y=$\sqrt{x-2}$+$\sqrt{2-x}$+$\frac{1}{4}$，则$\sqrt{{y^2}-4y+4}$-（x-2+$\sqrt{2}}$）2-z=-8$\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）解方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y+1}{3}=1}\\{3x+2y=2}\end{array}\right.$
    （2）解不等式组$\left\{\begin{array}{l}{5x+7＞3（x+1）}\\{\frac{1}{2}x-1≤1-\frac{3}{2}x}\end{array}\right.$
    并把解集在数轴上表示出来．

    查看答案和解析>>

    同步练习册答案