
 ����ƽ��ֱ������ϵ�У�����ֱ��
����ƽ��ֱ������ϵ�У�����ֱ��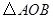 ��б��
��� ��
�� ���ϣ�����
���ϣ�����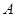 ������Ϊ
������Ϊ ��
��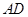 Ϊб���ϵĸߣ�������
Ϊб���ϵĸߣ������� ��ֱ��
��ֱ�� ���ڵ�
���ڵ� ����
���� �ĺ�����Ϊ
�ĺ�����Ϊ ����
����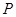 ��
�� ����������ϣ�����
����������ϣ�����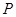 ��
�� �ᣮ������
�ᣮ������ �ڵ�
�ڵ� �����
�����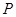 �ĺ�����Ϊ
�ĺ�����Ϊ ����
���� Ϊ������ı��ε����Ϊ
Ϊ������ı��ε����Ϊ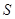 ��
��
 ����ֱ�ߵĽ���ʽ��
����ֱ�ߵĽ���ʽ�� ��ֵ��
��ֵ�� ʱ����
ʱ����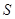 ��
�� �ĺ�����ϵʽ��
�ĺ�����ϵʽ�� ����ֱ��
����ֱ�� ������
������ �ڵ�
�ڵ� �����������ڵ�
�����������ڵ� ����
���� Ϊһ�ߣ���
Ϊһ�ߣ��� ���Ҳ�������
���Ҳ������� ������
������ ��ֱ��д������
��ֱ��д������ ��
�� �ص�����Ϊ��Գ�ͼ��ʱ
�ص�����Ϊ��Գ�ͼ��ʱ ��ȡֵ��Χ��
��ȡֵ��Χ��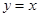 ����2��
����2��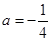 ����3����
����3����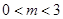 ʱ��
ʱ��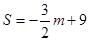 ����
����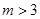 ʱ��S
ʱ��S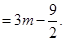
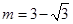 ��
��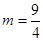 ��
�� .
.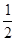 RN=
RN=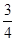 ����OP=OD-PD�������m��ֵ��
����OP=OD-PD�������m��ֵ��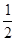 x֪��RD=
x֪��RD=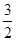 ����ʱR��AD���е㣬����RN��x�ᣬ��RN=
����ʱR��AD���е㣬����RN��x�ᣬ��RN=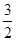 =
=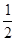 DB������N��ǡ��λ��AB�ϣ�RN�ǡ�ABD����λ�ߣ���ʱ�غϲ����ǵ���ֱ��������REN�����ڵ���ֱ������������Գ�ͼ�Σ����Դ������Ҳ�������⣬��ʱOP=OD=3����m=3��
DB������N��ǡ��λ��AB�ϣ�RN�ǡ�ABD����λ�ߣ���ʱ�غϲ����ǵ���ֱ��������REN�����ڵ���ֱ������������Գ�ͼ�Σ����Դ������Ҳ�������⣬��ʱOP=OD=3����m=3�� �Ľ���ʽΪ
�Ľ���ʽΪ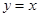 ��
��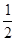 x=3��
x=3��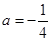 ��
��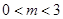 ʱ����ͼ�٣�
ʱ����ͼ�٣�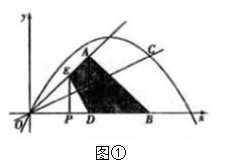
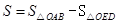 ��
��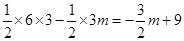 ��
��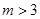 ʱ����ͼ�ڣ�
ʱ����ͼ�ڣ�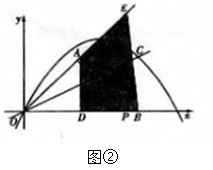

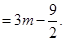
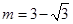 ��
��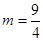 ��
�� .
.

 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ������A����1��0����B��3��0������
������A����1��0����B��3��0������ ���ڵ�C��MΪ�����ߵĶ��㣬����MB��
���ڵ�C��MΪ�����ߵĶ��㣬����MB��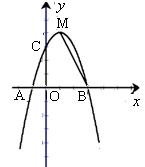
 �����Ƿ���ڵ�P�����PBM��ֱ�������Σ������ڣ������P������꣬�������ڣ���˵�����ɣ�
�����Ƿ���ڵ�P�����PBM��ֱ�������Σ������ڣ������P������꣬�������ڣ���˵�����ɣ� ����
���� �Ķ�����
�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
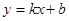 ��x���ڵ�A����1��0������y����B�㣬
��x���ڵ�A����1��0������y����B�㣬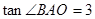 ����A��B����������߽�x������һ��C��3��0��.
����A��B����������߽�x������һ��C��3��0��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
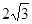 ������BCO=60�㣬OH��BC�ڵ�H������P�ӵ�H���������߶�HO���O�˶�������Q�ӵ�O���������߶�OA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ����P�˶���ʱ��Ϊt�룮
������BCO=60�㣬OH��BC�ڵ�H������P�ӵ�H���������߶�HO���O�˶�������Q�ӵ�O���������߶�OA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ����P�˶���ʱ��Ϊt�룮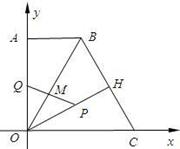
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
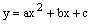 ��x�����һ����ΪA������ΪP���ҶԳ���Ϊֱ��x=2��
��x�����һ����ΪA������ΪP���ҶԳ���Ϊֱ��x=2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

| A���٢� | B���ڢ� | C���ۢ� | D���٢� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 �IJ���ͼ����ͼ��ʾ����y��0����
�IJ���ͼ����ͼ��ʾ����y��0���� ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A�� �� �� | B�� �� �� |
C�� | D�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com