
分析 ①易得新抛物线的顶点,根据平移转换可得原抛物线顶点,根据顶点式及平移前后二次项的系数不变可得原抛物线的解析式,展开即可得到b的值.
②根据关于x轴对称的点的坐标特点进行解答即可.
③根据关于y轴对称的点的坐标特点即可得出结论.
④根据图象绕与y轴的交点旋转180°,其对称轴不变,只是开口向下,即可得出图象的函数解析式.
解答 解:①由y=x2-2x+3=(x-1)2+2可知新抛物线的顶点为(1,2),
∴原抛物线的顶点为(-2,4),
设原抛物线的解析式为y=(x-h)2+k代入得:y=(x+2)2+4=x2+4x+8,
∴b=4.
故答案为4.
②∵关于x轴对称的点的坐标横坐标不变,纵坐标互为相反数,
∴函数y=x2-2x+3的图象沿x轴对折,得到的图象的解析式为-y=x2-2x+3,即y=-x2+2x-3.
故答案为:y=-x2+2x-3.
③∵关于y轴对称的点纵坐标不变,横坐标互为相反数,
∴抛物线y=x2-2x+3关于y轴对称的图象的解析式为y=(-x)2-2×(-x)+3,即y=x2+2x+3.
故答案为:y=x2+2x+3.
④因为二次函数y=x2-2x+3的图象绕它与y轴的交点旋转180°后,其对称轴不变,只是图象开口向下,因此二次函数新抛物线表达式为y=-x2-2x+3
故答案为:y=-x2-2x+3.
点评 此题主要考查了二次函数图象与几何变换,熟知平移的规律,关于x轴、y轴对称的点的坐标特点以及旋转的特征是解答此题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| h(千米) | 0 | 1 | 2 | 3 | 4 | … |
| t(℃) | 24 | 18 | 12 | 6 | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
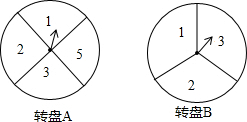 如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘游戏,游戏规则如下:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则欢欢胜;若指针所指两区域的数字之积为偶数,则乐乐胜;若有指针落在分割线上,则无效,重转.
如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘游戏,游戏规则如下:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则欢欢胜;若指针所指两区域的数字之积为偶数,则乐乐胜;若有指针落在分割线上,则无效,重转.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com