
【题目】对于平面直角坐标系![]() 中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
(1)当⊙O的半径为2时,
①如果点A(0,1),B(3,4),那么d(A,⊙O)=_______,d(B,⊙O)= ________;
②如果直线![]() 与⊙O互为“可及图形”,求b的取值范围;
与⊙O互为“可及图形”,求b的取值范围;
(2)⊙G的圆心G在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
【答案】(1)① 1,3;②![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1) ①根据图形M,N间的“近距离”的定义结合已知条件求解即可.
②根据可及图形的定义作出符合题意的图形,结合图形作答即可;
(2)分两种情况进行讨论即可.
(1)① 如图: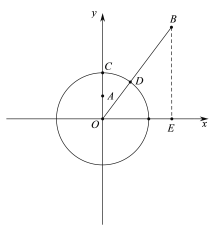
根据近距离的定义可知:d(A,⊙O)=AC=2-1=1.
过点B作BE⊥x轴于点E,则
OB=![]() =5
=5
∴d(B,⊙O)=OB-OD=5-2=3.
故答案为1,3.
② ∵由题意可知直线![]() 与⊙O互为“可及图形”,⊙O的半径为2,
与⊙O互为“可及图形”,⊙O的半径为2,
∴![]() .
.
∴![]() .
.
∴ ![]() .
.
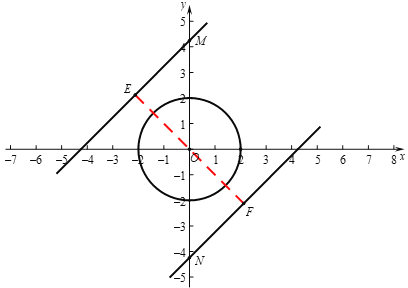
(2)①当⊙G与边OD是可及图形时,d(O,⊙G)=OG-1,
∴![]()
即-1≤m-1≤1
解得:![]() .
.
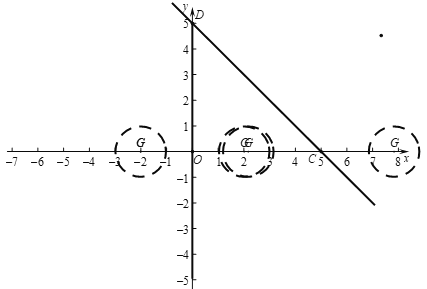
②当⊙G与边CD是可及图形时,如图,过点G作GE⊥CD于E,
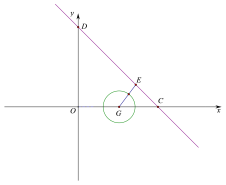
d(E,⊙G)=EG-1,
由近距离的定义可知d(E,⊙G)的最大值为1,
∴此时EG=2,
∵∠GCE=45°,
∴GC=2![]() .
.
∵OC=5,
∴OG=5-2![]() .
.
根据对称性,OG的最大值为5+2![]() .
.
∴![]()
综上所述,m的取值范围为:![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度。一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域。如图所示,AB=60![]() 海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120
海里,在B处测得C在北偏东45的方向上,A处测得C在北偏西30的方向上,在海岸线AB上有一灯塔D,测得AD=120![]() 海里。
海里。

(1)分别求出A与C及B与C的距离AC,BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,途中有无触礁的危险?
(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.45)
=2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图

根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在线段MN上存在点P、Q将线段MN分为相等的三部分,则称P、Q为线段MN的三等分点.
已知一次函数y=﹣x+3的图象与x、y轴分别交于点M、N,且A、C为线段MN的三等分点(点A在点C的左边).
(1)直接写出点A、C的坐标;
(2)①二次函数的图象恰好经过点O、A、C,试求此二次函数的解析式;
②过点A、C分别作AB、CD垂直x轴于B、D两点,在此抛物线O、C之间取一点P(点P不与O、C重合)作PF⊥x轴于点F,PF交OC于点E,是否存在点P使得AP=BE?若存在,求出点P的坐标?若不存在,试说明理由;
(3)在(2)的条件下,将△OAB沿AC方向移动到△O'A'B'(点A'在线段AC上,且不与C重合),△O'A'B'与△OCD重叠部分的面积为S,试求当S=![]() 时点A'的坐标.
时点A'的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.
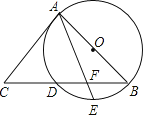
(1)求证:AC是⊙O的切线;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 抛物线
抛物线![]() 经过点
经过点![]() 、
、![]() .
.
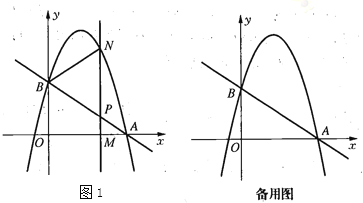
(1)求点![]() 的坐标和抛物线的解析式.
的坐标和抛物线的解析式.
(2)![]() 为
为![]() 轴上一个动点,过点
轴上一个动点,过点![]() 垂直于
垂直于![]() 轴的直线与直线
轴的直线与直线![]() 和抛物线分别交于点
和抛物线分别交于点![]() 、
、![]() .
.
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() 、
、![]() 、
、![]() 中恰有一点是其他两点所连线段的中点(三点重合除外),则称
中恰有一点是其他两点所连线段的中点(三点重合除外),则称![]() 、
、![]() 、
、![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() 、
、![]() 、
、![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ⊥AE于点O,点G,F分别在边CD,AB上,GF⊥AE.
①求证:DQ=AE;
②推断:![]() 的值为 ;
的值为 ;
(2)类比探究:如图(2),在矩形ABCD中,![]() =k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;
=k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接CP,当k=![]() 时,若tan∠CGP=
时,若tan∠CGP=![]() ,GF=2
,GF=2![]() ,求CP的长.
,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com