练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在平面直角坐标系中，抛物线的表达式为，线段AB的两个端点分别为A（1，2），B（3，2）

    （1）若抛物线经过原点，求出的值；

    （2）求抛物线顶点C的坐标（用含有m的代数式表示）；

    （3）若抛物线与线段AB恰有一个公共点，结合函数图象，求出m的取值范围.

    【答案】（1）（2）顶点C的坐标为；（3）m的取值范围为，

    【解析】

    （1）（0,0）代入即可解题,

    （2）将二次函数化为顶点式即可解题,

    （3）分类讨论确定m的取值范围,见详解.

    解：（1）∵抛物线经过原点,

    （2）

    所以，顶点C的坐标为

    （3）由顶点C的坐标可知，抛物线的顶点C在直线y=2x上移动．

    当抛物线过点A时，m=2或1；

    当抛物线过点B时，m=2或5．

    所以m=2时，抛物线与线段AB有两个公共点，不符合题意．

    结合函数的图象可知，m的取值范围为且

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

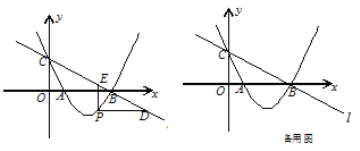
    【题目】如图，直线： 与轴、轴分别交于点B、C，经过B、C两点的抛物线与轴的另一个交点为A．

    （1）求该抛物线的解析式；

    （2）若点P在直线下方的抛物线上，过点P作PD∥轴交于点D，PE∥轴交于点E，

    求PD+PE的最大值；

    （3）设F为直线上的点，以A、B、P、F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】海南建省30年来，各项事业取得令人瞩目的成就，以2016年为例，全省社会固定资产总投资约3730亿元，其中包括中央项目、省属项目、地（市）属项目、县（市）属项目和其他项目．图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图，请完成下列问题：

    （1）在图1中，先计算地（市）属项目投资额为多少亿元，然后将条形统计图补充完整；

    （2）在图2中，县（市）属项目部分所占百分比为m%、对应的圆心角为β，求m的值，β等于多少度（m、β均取整数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

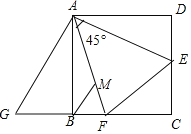
    【题目】已知如图，在正方形ABCD中，AD=4，E，F分别是CD，BC上的一点，且∠EAF=45°，EC=1，将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合，连接EF，过点B作BM∥AG，交AF于点M，则以下结论：①DE+BF=EF，②BF=，③AF=，④S△MEF=中正确的是　　

    A. ①②③ B. ②③④ C. ①③④ D. ①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下表显示的是某种大豆在相同条件下的发芽试验结果：

    每批粒数n

    100

    300

    400

    600

    1000

    2000

    3000

    发芽的粒数m

    96

    282

    382

    570

    948

    1904

    2850

    发芽的频率

    0.960

    0.940

    0.955

    0.950

    0.948

    0.952

    0.950

    下面有三个推断：

    ①当n为400时，发芽的大豆粒数为382，发芽的频率为0.955，所以大豆发芽的概率是0.955；

    ②随着试验时大豆的粒数的增加，大豆发芽的频率总在0.95附近摆动，显示出一定的稳定性，可以估计大豆发芽的概率是0.95；

    ③若大豆粒数n为4000，估计大豆发芽的粒数大约为3800粒．

    其中推断合理的是（　　）

    A. ①②③ B. ①② C. ①③ D. ②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC三个顶点的坐标分别是A（﹣3，1），B（﹣1，﹣1），C（2，2）．

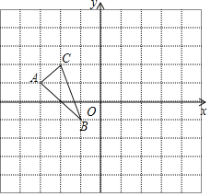
    （1）画出△ABC关于y轴对称的△A1B1C1，并写出点A1，B1，C1的坐标；

    （2）画出△ABC绕点B逆时针旋转90°所得到的△A2B2C2，并求出S．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：点A、C分别是∠B的两条边上的点，点D、E分别是直线BA、BC上的点，直线AE、CD相交于点P．

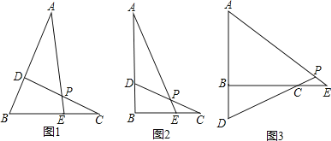
    （1）点D、E分别在线段BA、BC上；

    ①若∠B＝60°（如图1），且AD＝BE，BD＝CE，则∠APD的度数为　 　；

    ②若∠B＝90°（如图2），且AD＝BC，BD＝CE，求∠APD的度数；

    （2）如图3，点D、E分别在线段AB、BC的延长线上，若∠B＝90°，AD＝BC，∠APD＝45°，求证：BD＝CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，AB是⊙O的直径，C、D是⊙O上的点，且OC∥BD, AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD; ②∠AOC=∠AEC; ③CB平分∠ABD;④AF=DF; ⑤BD=2OF; ⑥△CEF ≌△BED,其中一定成立的是（ ）

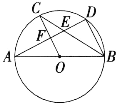
    A. ① ③ ⑤ ⑥ B. ① ③ ④ ⑤

    C. ② ④ ⑤ ⑥ D. ② ③ ④ ⑥

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=-x+4的图象与反比例函数y=（k为常数，且k≠0）的图象交于A（1，a），B两点．

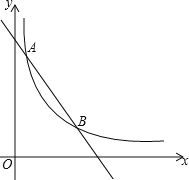
    （1）求反比例函数的表达式及点B的坐标；

    （2）结合图象直接写出不等式-x+4＞的解集

    （3）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．

    查看答案和解析>>

    同步练习册答案