
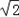 ),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1.
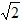 ,
,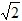 时,S=
时,S=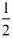 t2;
t2;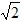 <t≤2
<t≤2 时,S=﹣
时,S=﹣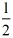 t2+2
t2+2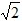 t﹣2;
t﹣2;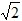 <t≤3
<t≤3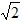 时,S=2;
时,S=2;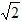 <t≤4
<t≤4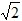 时 S=﹣
时 S=﹣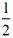 t2+3
t2+3 t﹣7;
t﹣7; <t≤5
<t≤5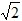 时,S=
时,S=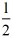 t2﹣5
t2﹣5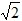 t+25;
t+25;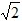 时,
时,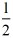 t2=1,解得:t=
t2=1,解得:t= ;
;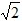 <t≤2
<t≤2 时,2﹣
时,2﹣ (2
(2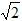 ﹣t)2=1,解得:t=
﹣t)2=1,解得:t=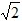 或3
或3 (舍去);
(舍去);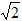 <t≤4
<t≤4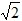 时,
时, (4
(4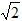 ﹣t)2=1,解得:t=3
﹣t)2=1,解得:t=3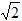 或5
或5 (5
(5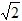 不合题意,舍去).
不合题意,舍去).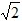 或3
或3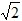 .
.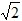 时,那么P位于CD中点处,P的坐标是:(2,2),
时,那么P位于CD中点处,P的坐标是:(2,2),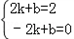 ,解得:
,解得: ,
,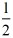 x+1,直线L表达式y=﹣x+2,
x+1,直线L表达式y=﹣x+2,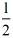 x+1中,令y=a,解得:x=2(a﹣1),
x+1中,令y=a,解得:x=2(a﹣1), ,
, 代入y=
代入y=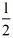 x+1中,解得:x=
x+1中,解得:x=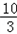 .
.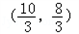 ;
; 时,P是AD与y轴的交点,则P的坐标是:(0,4).
时,P是AD与y轴的交点,则P的坐标是:(0,4).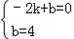 ,解得:
,解得: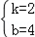 ,
, (a﹣4),
(a﹣4), (a﹣1);
(a﹣1);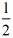 (a﹣4)﹣(2﹣a)=4,
(a﹣4)﹣(2﹣a)=4,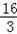 ,把y=
,把y=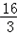 代入y=2x+4中,解得x=
代入y=2x+4中,解得x= .
. ,
,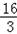 ).
). ,
, )或(
)或( ,
, ).
).

科目:初中数学 来源: 题型:
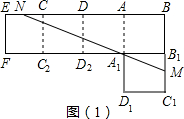
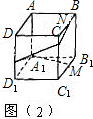
| 1 |
| MB |
| 1 |
| NB |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
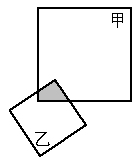
如图,甲、乙两个正方形纸片部分重叠在一起.已知重叠部分(阴影)面积与甲正方形面积之比是4∶21,重叠部分与乙正方形面积之比是3∶7.且甲正方形除阴影部分之外的面积是 ,则乙正方形的面积是多少平方厘米?
,则乙正方形的面积是多少平方厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1,
),C(2,0),固定正方形ABCD,直线L经过AC两点;将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1,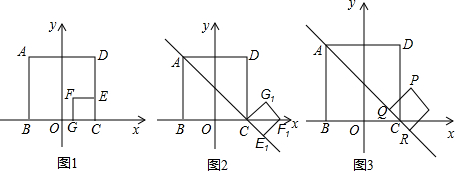
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com