
【题目】如图,四边形ABCD,已知∠A=90°,AB=3,BC=12,CD=13,DA=4.求四边形的面积. 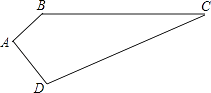
【答案】解:连接BD, ∵AB=3,BC=12,CD=13,DA=4,∠A=90°,
∵BD= ![]() =5,
=5,
∴BD2+BC2=CD2 ,
∴△BCD均为直角三角形,
∴S四边形ABCD的面积=S△ABD+S△BCD= ![]() ABAD+
ABAD+ ![]() BCBD=
BCBD= ![]() ×3×4+
×3×4+ ![]() ×12×5=36.
×12×5=36.
【解析】连接BD可得△ABD与△BCD均为直角三角形,进而可求解四边形的面积.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】一个小立方体的六个面分别标有字母A,B,C,D,E,F从三个不同方向看到的情形如图所示.
(1) A对面的字母是 ,B对面的字母是 ,E对面的字母是 .(请直接填写答案)

(2) 若A=2x-1,B=-3x+9.C=-7.D=1,E=4x+5,F=9,且字母A与它对面的字母表示的数互为相反数,求B,E的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
. 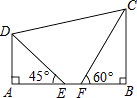
(1)BC= .
(2)求点D到BC的距离.
(3)求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象. 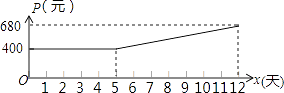
时间x(天) | 2 | 4 |
每天产量y(吨) | 24 | 28 |
(1)求药品每天的产量y(吨)是时间x(天)之间的函数关系式;
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格﹣成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com