
【题目】阅读理解题
定义:如果四边形的某条对角线平分一组角,那么把这条对角线叫“美妙线”,该四边形叫做“美妙四边形”.
如图:在四边形ABCD中,对角线BC平分∠ACD和∠ABD,那么对角线BC叫“美妙线”,四边形ABCD就称为“美妙四边形”.
问题:(1)下列四边形中是“美妙四边形”的有_______个.
①平行四边形 ②矩形 ③菱形 ④正方形
A.1 B. 2 C. 3 D.4
(2)四边形ABCD是“美妙四边形”,AB=3+![]() ,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.
,∠BAD=60°,∠ABC=90°,求四边形ABCD的面积.
(3)如图,若△ABC中,AB=3,BC=4,∠B=90°,将△ABC扩充成以AC为“美妙线”的“美妙四边形”ABCD,试求D到BC的距离.

【答案】(1)B;(2)①S=![]() ②S=
②S=![]() ;(3)
;(3)![]()
【解析】
(1)根据“美妙四边形”的定义,结合平行四边形,矩形,菱形 ,正方形的性质即可判断.
(2)分①当AC是美妙线时和②当BD是美妙线时,两种情况进行讨论.
(3)如图,过D作MN∥BC交BA延长线于点M且CN⊥MN,证明△MDA∽△NCD
根据相似三角形的性质得到![]() 设AM=3x,则DN=4x,MD=4-4x,CN=3x+3,得到,
设AM=3x,则DN=4x,MD=4-4x,CN=3x+3,得到,![]() 解方程求出
解方程求出![]() 的值,即可求解.
的值,即可求解.
.解:(1)菱形和正方形是“美妙四边形”.
故答案为:B
(2)①当AC是美妙线时,如图
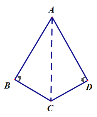
AB=3+![]() ,∠BAD=60°,
,∠BAD=60°,
![]()
![]()
![]() ,
,
![]() ,
,
②当BD是美妙线时,如图,过D作DH⊥AB,![]()
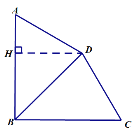
设AH=a,则![]()
∴![]()
∴![]()
∴DH=3,
![]()
![]() ,
,
综上所述:S=![]() 或
或![]()
(3)如图,过D作MN∥BC交BA延长线于点M且CN⊥MN
由题意,得∠M=∠N=90°

∠MDA+∠MAD=90°
∠MDA+∠CDN=90°
∴∠MAD=∠CDN
∴△MDA∽△NCD
![]()
设AM=3x,则DN=4x,MD=4-4x,CN=3x+3
![]()
∴x=![]() ,
,
∴DH=3x+3=![]()


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费4元;方式二:不购买会员证,每次游泳付费10元.设小明计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 140 | 160 | _______ | … | _______ |
方式二的总费用(元) | 100 | 150 | ________ | … | ________ |
(2)若小明计划今年夏季游泳的总费用为260元,选择哪种付费方式,他游泳的次数比较多?
(3)小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
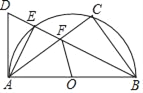
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且∠DAE=∠FAE.
(1)求证:AD为⊙O切线;
(2)若sin∠BAC=![]() ,求tan∠AFO的值.
,求tan∠AFO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分) 青少年沉迷于手机游戏,严重危害他们的身心健康,此问题已引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的“王者荣耀”玩家进行了简单的随机抽样调查,绘制出以下两幅统计图.
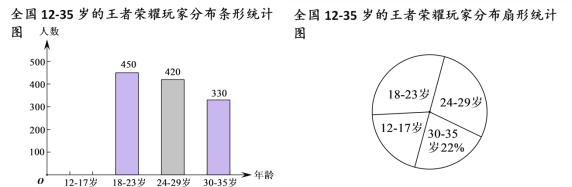
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是_________;
(3)据报道,目前我国12﹣35岁“王者荣耀”玩家的人数约为2000万,请估计其中12﹣23岁的人数.
(4)根据对统计图表的分析,请你为沉迷游戏的同学提一个合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为![]() ”的尺规作图过程.
”的尺规作图过程.
已知:![]() .求作:矩形
.求作:矩形![]() ,使得矩形
,使得矩形![]() 内接于
内接于![]() ,且其对角线
,且其对角线![]() 的夹角为
的夹角为![]() .
.
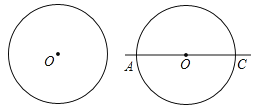
作法:如图,
①作![]() 的直径
的直径![]() ;
;
②以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交直线
长为半径画弧,交直线![]() 上方的圆弧于点
上方的圆弧于点![]() ;
;
③连接![]() 并延长交
并延长交![]() 于点
于点![]() ;
;
④连接![]() .
.
所以四边形![]() 就是所求作的矩形,根据小东设计的尺规作图过程,
就是所求作的矩形,根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹).
(2)完成下面的证明.
证明:∵点![]() 都在
都在![]() 上,
上,
∴![]() .
.
同理![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ( )(填推理的依据).
( )(填推理的依据).
∴四边形![]() 是矩形.
是矩形.
∵![]()
![]() ,
,
∴![]() .
.
∴四边形![]() 是所求作的矩形.
是所求作的矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P和图形W,如果以P为端点的任意一条射线与图形W最多只有一个公共点,那么称点P独立于图形W.
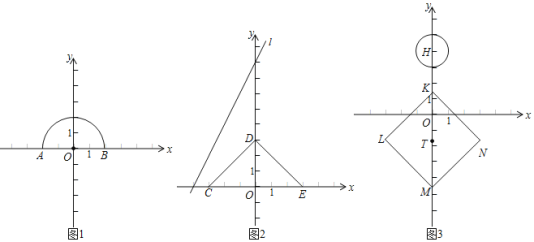
(1)如图1,已知点A(-2,0),以原点O为圆心,OA长为半径画弧交x轴正半轴于点B.在P1(0,4),P2(0,1),P3(0,-3),P4(4,0)这四个点中,独立于![]() 的点是 ;
的点是 ;
(2)如图2,已知点C(-3,0),D(0,3),E(3,0),点P是直线l:y=2x+8上的一个动点.若点P独立于折线CD-DE,求点P的横坐标xp的取值范围;
(3)如图3,⊙H是以点H(0,4)为圆心,半径为1的圆.点T(0,t)在y轴上且t>-3,以点T为中心的正方形KLMN的顶点K的坐标为(0,t+3),将正方形KLMN在x轴及x轴上方的部分记为图形W.若⊙H上的所有点都独立于图形W,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点P在一次函数![]() 图象上,点Q在反比例函数
图象上,点Q在反比例函数![]() 图象上,若存在点P与点Q关于原点对称,我们称二次函数
图象上,若存在点P与点Q关于原点对称,我们称二次函数![]() 为一次函数
为一次函数![]() 与反比例函数
与反比例函数![]() 的“新时代函数”,点P称为“幸福点”。
的“新时代函数”,点P称为“幸福点”。
(1)判断![]() 与
与![]() 是否存在“新时代函数”,如果存在,请求出“幸福点”坐标,如果不存在,请说明理由;
是否存在“新时代函数”,如果存在,请求出“幸福点”坐标,如果不存在,请说明理由;
(2)若反比例函数![]() 与一次函数
与一次函数![]() 有两个“幸福点”,
有两个“幸福点”,![]() 和
和![]() ,且
,且![]() ,求其“新时代函数”的解析式;
,求其“新时代函数”的解析式;
(3)若一次函数![]() 和反比例函数
和反比例函数![]() 在自变量x的值满足
在自变量x的值满足![]() 的情况下,其“新时代函数”的最小值为3,求m的值。
的情况下,其“新时代函数”的最小值为3,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 点,与
点,与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,且点
两点,且点![]() 在点
在点![]() 的右侧,设抛物线的顶点为
的右侧,设抛物线的顶点为![]() .
.
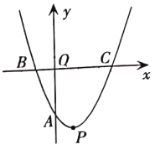
(1)若点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)当![]() 时,该抛物线上最高点与最低点纵坐标的差为
时,该抛物线上最高点与最低点纵坐标的差为![]() ,求出
,求出![]() 与
与![]() 的关系;若
的关系;若![]() 有最大值或最小值,直接写出这个最大值或最小值.
有最大值或最小值,直接写出这个最大值或最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com