
分析 (1)此题分两种情况考虑:一是b和c中有一个和a相等,是2;二是b=c,即根据方程有两个相等的实数根,由△=0求解.最后注意看是否符合三角形的三边关系.
(2)根据(1)中求解的结果,只需求得2,2,1的三角形的内切圆的半径,根据等腰三角形的三线合一和勾股定理求解.
解答 解:(1)若b、c中有一边等于2,
则方程可化为22+2(m-1)-m=0,
解得m=-2;
原方程可化为x2-3x+2=0,
解得x1=1,x2=2,
所以三角形的周长为2+2+1=5;
若b=c,则△=(m-1)2+4m=0,
解得m=-1,
当m=-1时,方程为x2-2x+1=0,得x1=x2=1(不合题意,舍去),
所以三角形的周长为2+2+1=5;
综上可知△ABC的周长为5.
(2)作△ABC的内切圆⊙O,连接AO并延长交⊙O于点D,
连接BO,CO,过点O作OA⊥AB,OF⊥AC.
∴BD=CD,BD⊥CD,
∵AB=AC=2,BD=CD=$\frac{1}{2}$,
∴AD=$\frac{\sqrt{15}}{2}$,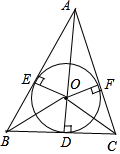 ∵S△ABC=S△OAB+S△OAC+S△OBC,
∵S△ABC=S△OAB+S△OAC+S△OBC,
∴$\frac{1}{2}$BC•AD=$\frac{1}{2}$AB•OE+$\frac{1}{2}$AC•OF+$\frac{1}{2}$BC•OD,
即$\frac{\sqrt{15}}{2}$=2r+2r+r,
∴r=$\frac{\sqrt{15}}{10}$,
△ABC的内切圆半径为$\frac{\sqrt{15}}{10}$.
点评 本题考查了三角形的内切圆与内心,注意(1)中的多种情况,能够熟练结合等腰三角形的三线合一和勾股定理求得等腰三角形的内切圆的半径.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
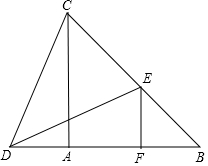 如图,在△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=CD,EF∥AC,交AB于点F.
如图,在△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=CD,EF∥AC,交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | 2x+1=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.
如图,△ABC与△AED中,∠E=∠C,DE=BC,EA=CA,过A作AF⊥DE垂足为F,DE交CB的延长线于点G,连接AG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com