练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知A=$\frac{9{9}^{9}}{{9}^{99}}$，B=$\frac{1{1}^{9}}{{9}^{90}}$，请判断A、B的大小．

    分析 直接利用幂的乘方运算法则将A式变形进而得出答案．

    解答 解：∵A=$\frac{9{9}^{9}}{{9}^{99}}$=$\frac{{9}^{9}×1{1}^{9}}{（{9}^{9}）^{11}}$=$\frac{1{1}^{9}}{（{9}^{9}）^{10}}$=$\frac{1{1}^{9}}{{9}^{90}}$，
    ∴A=B．

    点评 此题主要考查了幂的乘方运算，正确利用幂的乘方运算法则化简A式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．已知实数a满足|2016-a|+$\sqrt{a-2017}$=a，那么a-20162的值是（　　）
    A．2015B．2016C．2017D．2018

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

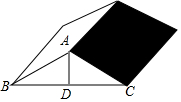    13．如图所示是某工厂长方屋顶的人字架（等腰三角形），它的跨度BC=12米，中柱AD为2.5米，中柱AD⊥BC，且垂足D为BC的中点，又知厂房长20米，为防雨，需在房顶铺满油毡．（每卷油毡宽1米，长10米），如果你是该厂采购，需购买多少卷油毡？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图：线段AB、CD相交于点O，连接AD、CB，我们把这个图形称为“8字型”．根据三角形内角和容易得到：∠A+∠D=∠C+∠B．

    （1）用“8字型”
    如图（1）：∠A+∠B+∠C+∠D+∠E+∠F=360°．
    （2）造“8字型”
    如图（2）：∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°．
    （3）发现“8字型”
    如图（3）：BE、CD相交于点A，CF为∠BCD的平分线，EF为∠BED的平分线．
    ①图中共有6个“8字型”；
    ②若∠B：∠D：∠F=4：6：x，求x的值．

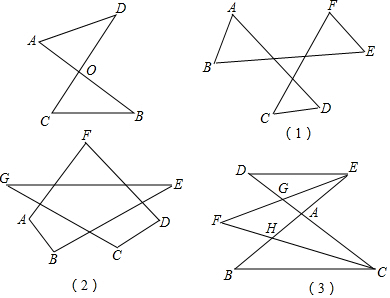
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

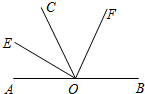    17．如图，O为直线AB上一点，作射线OC，OE平分∠AOC，OF平分∠BOC．
    （1）试判断OE与OF的位置关系，并说明理由；
    （2）若∠COF：∠EOB=2：5，求∠AOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

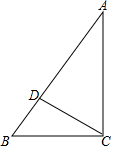    7．如图，在Rt△ABC中，∠ACB=90°，点D在AB上，将△BCD绕点C按顺时针方向旋转90°后得△ECF．
    （1）补充完成图形；
    （2）若EF∥CD，求证：∠BDC=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

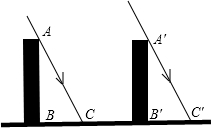    14．如图，太阳光线AC与A′C′是平行的，同一时刻垂直于地面的两根木杆在太阳光照射下的影子一样长，那么这辆跟木杆高度相同吗？
    小明思考过程如下：（请在括号内填上理由）
    因为AC∥A′C′．（①已知）
    所以∠ACB=∠A′C′B′．（②两直线平行，同位角相等）
    在△ABC和△A′B′C′中．
    因为∠ABC=∠A′B′C′=90°，BC=B′C′，∠ACB=∠A′C′B′．
    所以△ABC≌△A′B′C′．（③ASA）
    所以AB=A′B′（④全等三角形对应边相等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

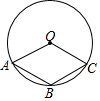    11．如图，已知点A，B，C均在⊙O上，并且四边形OABC是菱形，那么∠AOC与2∠OAB之间的关系是（　　）
    A．∠AOC＞2∠OABB．∠AOC=2∠OABC．∠AOC＜2∠OABD．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列二次根式中，最简二次根式是（　　）
    A．$\sqrt{5{a}^{2}}$B．$\sqrt{\frac{1}{2}}$C．$\sqrt{2.5}$D．$\sqrt{{a}^{2}-{b}^{2}}$

    查看答案和解析>>

    同步练习册答案