
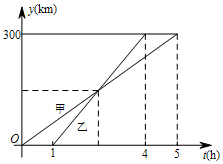
 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.以上结论正确的是①②.
甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,$t=\frac{5}{4}$或$\frac{15}{4}$.以上结论正确的是①②. 分析 观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,进而得出答案.
解答 解:由图象可知,A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得,k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得
$\left\{\begin{array}{l}{m+n=0}\\{4m+n=300}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=100}\\{n=-100}\end{array}\right.$,
∴y乙=100t-100,
令y甲=y乙可得:60t=100t-100,
解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲-y乙|=50,可得|60t-100t+100|=50,即|100-40t|=50,
当100-40t=50时,可解得t=$\frac{5}{4}$,
当100-40t=-50时,可解得t=$\frac{15}{4}$,
又当t=$\frac{5}{6}$时,y甲=50,此时乙还没出发,
当t=$\frac{25}{6}$时,乙到达B城,y甲=250;
综上可知当t的值为$\frac{5}{4}$或$\frac{15}{4}$或$\frac{5}{6}$或t=$\frac{25}{6}$时,两车相距50千米,
∴④不正确;
综上,正确的有①②,
故答案为:①②
点评 本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意t是甲车所用的时间.


科目:初中数学 来源: 题型:解答题
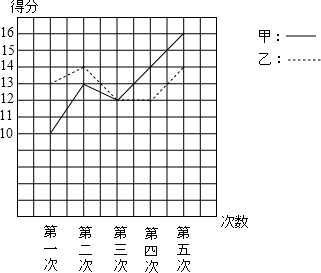 如图是甲、乙两位同学参加某体育项目训练,近期五次测试成绩得分情况.
如图是甲、乙两位同学参加某体育项目训练,近期五次测试成绩得分情况.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a<\frac{1}{a}<{a^2}$ | B. | $\frac{1}{a}<a<{a^2}$ | C. | $a<{a^2}<\frac{1}{a}$ | D. | ${a^2}<a<\frac{1}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为8cm,则△DOE的周长是( )
如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为8cm,则△DOE的周长是( )| A. | 8cm | B. | 6cm | C. | 4cm | D. | 2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com