
【题目】如图所示,在△ABC中,![]() 是
是![]() 边上的中点,
边上的中点,![]() ,请你添加一个条件,使
,请你添加一个条件,使![]() 成立.你添加的条件是_______________(不再添加辅助线和字母).
成立.你添加的条件是_______________(不再添加辅助线和字母).

【答案】本题答案不唯一,可添加条件:∠B=∠C或AB=AC或∠BED=∠CFD.
【解析】
根据“全等三角形的判定方法”结合已知条件分析解答即可.
由题意可知,当△BDE≌△CDF时,DE=DF.
∵在△BDE和△CDF中,由题意可知已经有DB=DC,∠BDE=∠CDF一边一角对应相等,
∴(1)当添加条件:∠B=∠C时,可由“ASA”证得△BDE≌△CDF,即可得到DE=DF;
(2)当添加条件:AB=AC时,可得∠B=∠C,这样由“ASA”证得△BDE≌△CDF,即可得到DE=DF;
(3)当添加条件:∠BED=∠CFD时,可由“AAS”证得△BDE≌△CDF,由此可得DE=DF;
综上所述,本题答案不唯一,可添加条件:∠B=∠C或AB=AC或∠BED=∠CFD.
故答案为:本题答案不唯一,可添加条件:∠B=∠C或AB=AC或∠BED=∠CFD.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.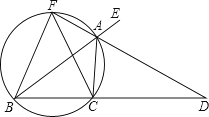
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ![]() ,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为( ) 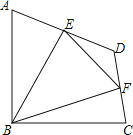
A.2
B.![]()
C.![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB= ![]() ,E是
,E是 ![]() 的中点,求EGED的值.
的中点,求EGED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:
蔬菜品种 | 西红柿 | 青椒 | 西兰花 | 豆角 |
批发价(元/kg) | 3.6 | 5.4 | 8 | 4.8 |
零售价(元/吨) | 5.4 | 8.4 | 14 | 7.6 |
请解答下列问题:
(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300 kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?
(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后赚钱数1050元,则该经营户批发西红柿多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作分母为1的有理数;反之为无理数.如![]() 不能表示为两个互质的整数的商,所以
不能表示为两个互质的整数的商,所以![]() 几个号无理数.可以这样证明:
几个号无理数.可以这样证明:
设![]() ,a与b是互质的两个整数,且b≠0,则2=
,a与b是互质的两个整数,且b≠0,则2=![]() ,所以a=2b.
,所以a=2b.
因为b是整数且不为0,所以a是不为0的偶数.设a=2n(n是整数),
所以b=2n,所以b也是偶数,与a与b是互质的整数矛盾,
所以![]() 是无理数.
是无理数.
仔细阅读上文,然后请证明:![]() 是无理数。
是无理数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com