
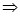 ★”表示.并给出证明;我的命题是: .
★”表示.并给出证明;我的命题是: .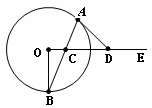
科目:初中数学 来源: 题型:
 24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是:
24、如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:①DA是⊙O的切线;②DA=DC;③OD⊥OB.请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,用“★★?★”表示.并给出证明.我的命题是:查看答案和解析>>
科目:初中数学 来源:2013届福建仙游高峰初级中学九年级上学期期中考试数学试题(带解析) 题型:解答题
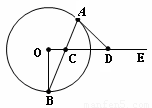
如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断: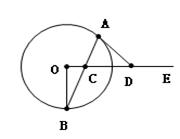
(1)DA是⊙O的切线;(2)DA=DC;(3)OD⊥OB。
请以其中两个为条件,另一个为结论,写出一个真命题,用“○○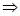 ○”表示。并证明。
○”表示。并证明。
我的是: 。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建仙游高峰初级中学九年级上学期期中考试数学试题(解析版) 题型:解答题
如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断:

(1)DA是⊙O的切线;(2)DA=DC;(3)OD⊥OB。
请以其中两个为条件,另一个为结论,写出一个真命题,用“○○ ○”表示。并证明。
○”表示。并证明。
我的是: 。
查看答案和解析>>
科目:初中数学 来源:2012届江苏省九年级下学期期中考试数学卷(解析版) 题型:解答题
如图,C是射线 OE上的一动点,AB是过点 C的弦,直线DA与OE的交点为D,现有三个论断: ①DA是⊙O的切线;②DA=DC;③ OD⊥OB.
请你以其中的两个论断为条件,另一个论断为结论,用序号写出一个真命题,
用“★★ ★”表示.并给出证明;我的命题是:
.
★”表示.并给出证明;我的命题是:
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com