

 ×100%=50%;
×100%=50%;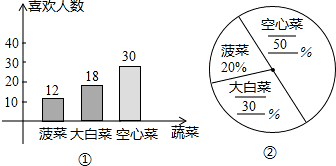


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北潜江、仙桃、天门、江汉油田卷)数学(解析版) 题型:解答题
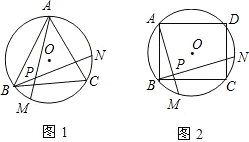
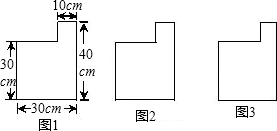
一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.如图1,矩形ABCD中,若AB=2,BC=6,则称矩形ABCD为2阶奇异矩形.
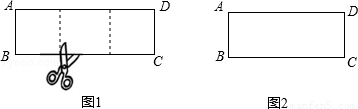
(1)判断与操作:
如图2,矩形ABCD长为5,宽为2,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(2)探究与计算:
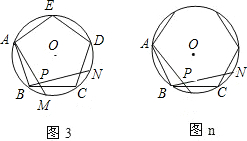
已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方写出a的值.
(3)归纳与拓展:
已知矩形ABCD两邻边的长分别为b,c(b<c),且它是4阶奇异矩形,求b:c(直接写出结果).
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前知识点回归+巩固 专题13 二次函数(解析版) 题型:解答题
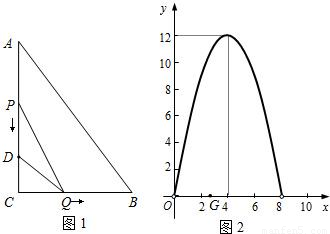
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com