
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称次抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
【答案】(1)“带线”L的表达式为y=2x2+4x﹣4;(2)m=2,n=﹣2;(3)点P的坐标为(![]() ,
, ![]() ).
).
【解析】试题分析:
(1)由“路线l”的表达式为:y=2x-4可得,“路线l”与y轴交于点(0,-4);把x=-1代入y=2x-4可得y=-6,由此可得“带线L”的顶点坐标为(-1,-6),结合“带线L”过点(0,-4)即可求得“带线L”的解析式;
(2)由y=mx2﹣2mx+m﹣1=m(m-1)2-1可得“带线L”的顶点坐标为(1,-1),与y轴交于点(0,m-1),把这两个点的坐标代入y=nx+1即可求得m、n的值;
(3)如图,由(2)可知,若设“带线L”的顶点为B,则点B坐标为(1,﹣1),过点B作BC⊥y轴于点C,连接PA并延长交x轴于点D,由⊙P与“路线”l相切于点A可得PD⊥l于点A,由此证Rt△AOD≌Rt△BCA即可求得点D的坐标,结合点A的坐标即可求得AD的解析式为y=![]() x+1,由AD的解析式和“带线L”的解析式组成方程组,解方程组即可求得点P的坐标.
x+1,由AD的解析式和“带线L”的解析式组成方程组,解方程组即可求得点P的坐标.
试题解析:
((1)∵“带线”L的顶点横坐标是﹣1,且它的“路线”l的表达式为y=2x﹣4
∴y=2×(﹣1)﹣4=﹣6,
∴“带线”L的顶点坐标为(﹣1,﹣6).
设L的表达式为y=a(x+1)2﹣6,
∵“路线”y=2x﹣4与y轴的交点坐标为(0,﹣4)
∴“带线”L也经过点(0,﹣4),将(0,﹣4)代入L的表达式,解得a=2
∴“带线”L的表达式为 y=2(x+1)2﹣6=2x2+4x﹣4;
(2)∵直线y=nx+1与y轴的交点坐标为(0,1),
∴抛物线y=mx2﹣2mx+m﹣1与y轴的交点坐标也为(0,1),解得m=2,
∴抛物线表达式为y=2x2﹣4x+1,其顶点坐标为(1,﹣1)
∴直线y=nx+1经过点(1,﹣1),解得n=﹣2;
(3)如图,设“带线L”的顶点为B,则点B坐标为(1,﹣1),过点B作BC⊥y轴于点C,
∴∠BCA=90°,
又∵点A 坐标为(0,1),
∴AO=1,BC=1,AC=2.
∵“路线”l是经过点A、B的直线
且⊙P与“路线”l相切于点A,连接PA交 x轴于点D,
∴PA⊥AB,
∴∠DAB=∠AOD=90°,
∴∠ADO+∠DAO=90°,
又∵∠DAO+∠BAC=90°,
∴∠ADO=∠BAC,
∴Rt△AOD≌Rt△BCA,
∴OD=AC=2,
∴D点坐标为(﹣2,0)
∴经过点D、A的直线表达式为y=![]() x+1,
x+1,
∵点P为直线y=![]() x+1与抛物线L:y=2x2﹣4x+1的交点,
x+1与抛物线L:y=2x2﹣4x+1的交点,
解方程组: 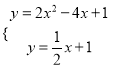 得 :
得 : ![]() (即点A舍去),
(即点A舍去),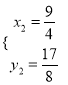 ,
,
∴点P的坐标为![]() .
.
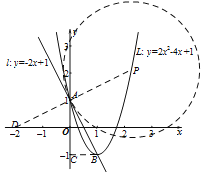


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,,商场一天可获利润y元.
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段引导市民节约用水。某市规定如下用水收费标准:每月每户的用水不超过6![]() 时,水费按正常收费;超过6
时,水费按正常收费;超过6![]() 时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9
时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9![]() ,缴纳水费为27元;3月份的用水量为11
,缴纳水费为27元;3月份的用水量为11![]() ,缴纳水费为37元。
,缴纳水费为37元。
(1)求在限定量以内每吨多少元?超出部分的水费每吨多少元?
(2)若该市某居民今年4月份的用水量为13![]() . 则应缴纳水费多少元?
. 则应缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成一项工作,如果安排两个人合做,要![]() 天才能完成.开始先安排一些人做
天才能完成.开始先安排一些人做![]() 天后,又增加
天后,又增加![]() 人和他们一起做
人和他们一起做![]() 天,结果完成了这项工作的一半,假设这些人的工作效率相同.
天,结果完成了这项工作的一半,假设这些人的工作效率相同.
(1)开始安排了多少名工人?
(2)如果要求再用![]() 天做完剩余的全部工作,还需要再增加几人一起做?
天做完剩余的全部工作,还需要再增加几人一起做?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若a,b互为相反数,则![]() =-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为
=-1;②若a+b<0,ab>0,则|a+2b|=-a-2b;③若多项式ax3+bx+1的值为5,则多项式-ax3-bx+1的值为-3;④若甲班有50名学生,平均分是a分,乙班有40名学生,平均分是b分,则两班的平均分为![]() 分.其中正确的为____(填序号).
分.其中正确的为____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1=![]() ,
,
第2个等式:a2=![]() ,
,
第3个等式:a3=![]() ,
,
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= = ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)求a1+a2+a3+…+a2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平移和翻折是初中数学两种重要的图形变化.
(1)平移运动
①把笔尖放在数轴的原点处,先向负方向移动3个单位长度,再向正方向移动![]() 个单位长度,这时笔尖的位置表示什么数?用算式表示以上过程及结果是( )
个单位长度,这时笔尖的位置表示什么数?用算式表示以上过程及结果是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
②一机器人从原点O开始,第1次向左跳1个单位,紧接着第2次向右跳2个单位,第3次向左跳3个单位,第4次向右跳4个单位,……,依次规律跳,当它跳2019次时,落在数轴上的点表示的数是_____.
(2)翻折变换
①若折叠纸条,表示-1的点与表示3的点重合,则表示2019的点与表示_______的点重合.
![]()
②若数轴上A、B两点之间的距离为2019(A在B的左侧,且折痕与①折痕相同),且A、B两点经折叠后重合,则A点表示_____B点表示______.
③若数轴上折叠重合的两点的数分别为a,b,折叠中间点表示的数为____.(用含有a,b的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com