Question

（A）已知四边形ABCD中，AD∥BC，对角线AC、BD交于点O，∠OBC=∠OCB，并且________，求证：四边形ABCD是________形．（要求在已知条件中的横线上补上一个条件________，在求证中的横线上添上该四边形的形状，然后画出图形，予以证明，证明时要用上所有条件）
（B）某市市委、市府2001年提出“工业立市”的口号，积极招商引资，财政收入稳步增长，各年度财政收入如下表：

年 份	2001	2002	2003	2004	…
财政收入 单位（亿元）	10	10.5	12	14.5	…

按这种增长趋势，请你算一算2006年该市的财政收入是多少亿元．

Answer 1

AD=CB    矩    AD=CB
分析：A、当AD=CB，四边形ABCD是矩形：根据题意证得四边形ABCD为平行四边形，根据平行四边形的性质，即可得OB=BD，OC=AC，又由等角对等边，易证得AC=BD，即可得四边形ABCD为矩形；
B、由四点：（1，10），（2，10.5），（3，12），（4，14.5），可判断财政收入与年份大致为二次函数关系，然后设y=ax²+bx+c，利用待定系数法即可求得此二次函数的解析式，继而求得2006年该市的财政收入．
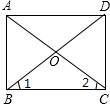解答：（A）解：AD=CB，矩形．
证明：∵AD∥BC，AD=BC，
∴四边形ABCD为平行四边形，
∴OB=BD，OC=AC，
又∵∠1=∠2，
∴OB=OC，
∴AC=BD，
∴四边形ABCD为矩形．
（B）解：2001作为第一年，分别得四点：
（1，10），（2，10.5），（3，12），（4，14.5），
判断财政收入与年份大致为二次函数关系．
设：y=ax²+bx+c，
10=a+b+c，a=，
则  10.5=4a+2b+c，
解得：b=-1，
12=9a+3b+c，
∴c=10.5，
∴y=x²-x+10.5，
当x=6时，y=22.5（亿元）
∴2006年财政收入将达到22.5亿元．（说明：若不画图象推断，但结果正确也得分）
点评：此题考查了矩形的判定，平行四边形的判定与性质以及二次函数的实际应用．此题综合性很强，难度较大，解题的关键是注意数形结合思想与方程思想的应用．