Question

在Rt△ABC中，∠ACB=90°，∠A=30°，BC=.动点O在AC上，以点O为圆心，OA长为半径的⊙O分别交AB、AC于点D、E，连结CD.

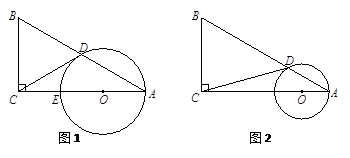
1.如图1，当直线CD与⊙O相切时，请你判断线段CD与AD的数量关系，并证明你的结论；

2.如图2，当∠ACD=15°时，求AD的长

 

Answer 1

 

1.CD=AD       ……1分

证明：如图1，连结OD．

∵直线CD与⊙O相切．∴∠COD＝90°，……2分

又∵ OD＝OA，    ∴  ∠A=∠ADO＝30°．

∴  ∠COD=60°．∴ ∠ACD=30°．   ……3分

∴CD=AD，…………4分

2.如图2，过点C作CF⊥AB于点F．

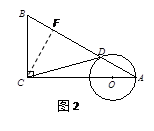
∵ ∠A＝30°，BC=，∴ AB=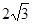．   ……5分

∵ ∠ACD＝15°，∴ ∠BCD＝75°，∠BDC＝45°．……6分

  在Rt△BCF中，可求BF=，CF=．    

  在Rt△CDF中，可求DF＝．       ……7分

  ∴ AD＝AB－BF-FD＝－－＝ (－3)．……8分

解析:（1）直线CD与⊙O相切，连接OD，可得∠CDO=90°，则CD=BD．

（2）过点C作CF⊥AB于点F，根据已知条件，可求出在三角形ABC中，AB=4．又∠BDC=45°，所以△DCF为等腰直角三角形，DF=CF，在Rt△BCF中，可求BF=，CF=3=DF，所以AD可用求差法进行求解