
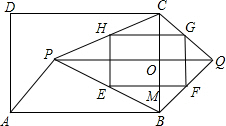
 如图,点P为矩形ABCD内一点,作平行四边形ABQP,连接CP、CQ、BP,E、F、G、H分别是BP、BQ、CQ、CP的中点,
如图,点P为矩形ABCD内一点,作平行四边形ABQP,连接CP、CQ、BP,E、F、G、H分别是BP、BQ、CQ、CP的中点,| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2014年中考数学二轮精品复习动点型问题练习卷(解析版) 题型:解答题
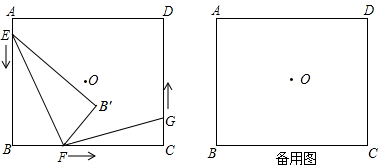
如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).
(1)当t= ????????? s时,四边形EBFB′为正方形;
(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
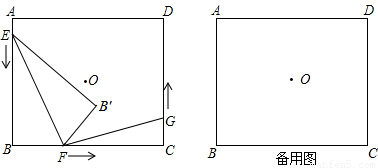
如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
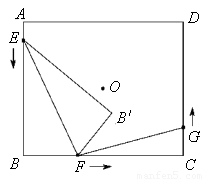
(1)当t= s时,四边形EBFB'为正方形;
(2)若以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012年湖北省武汉市中考数学模拟试卷(四)(解析版) 题型:解答题
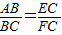 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com