如图.AD∥BC.BD平分∠ABC．求证:AB=AD．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

如图，AD∥BC，BD平分∠ABC．求证：AB=AD．

证明：∵AD∥BC，∴∠ADB=∠DBC。
∵BD平分∠ABC，∴∠ABD=∠DBC。
∴∠ABD=∠ADB。∴AB=AD。

解析试题分析：根据AD∥BC，可求证∠ADB=∠DBC，利用BD平分∠ABC和等量代换可求证∠ABD=∠ADB，然后即可得出结论。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

如图，已知四边形ABCD，AD∥BC．点P在直线CD上运动（点P和点C，D不重合，点P，A，B不在同一条直线上），若记∠DAP，∠APB，∠PBC分别为．
（1）当点P在线段CD上运动时，写出之间的关系并说出理由；
（2）如果点P在线段CD（或DC）的延长线上运动，探究之间的关系，并选择其中的一种情况说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

如图所示，C、D是线段AB的三等分点，且AD=4，求AB的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

如图，∠1=∠2，∠1+∠2=162°，求∠3与∠4的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

如图，点D、E、F分别在AB、BC、AC上，且DE//AC，EF//AB ，下面写出了证明“∠A+∠B+∠C=180°”的部分过程，请完成填空：

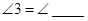DE // AC，EF // AB (              )
，(             )
EF // AB.
(                )
DE // AC.
(                 )
(                )

.