
分析 (1)根据方程的系数结合根的判别式即可得出△=1>0,由此即可得出方程有两个不相等的实数根;
(2)根据根与系数的关系进行解答;
(3)利用分解因式法可求出x1=k+1,x2=k+2.①不妨设AB=k+1,AC=k+2,根据BC=5利用勾股定理即可得出关于k的一元二次方程,解方程即可得出k的值;②根据(1)结论可得出AB≠AC,由此可找出△ABC是等腰三角形分两种情况,分AB=BC、AC=BC两种情况考虑,根据两边相等找出关于k的一元一次方程,解方程求出k值,进而可得出三角形的三边长,再根据三角形的周长公式即可得出结论
解答 解:(1)∵在方程x2-(2k+3)x+k2+3k+2=0中,△=b2-4ac=[-(2k+3)]2-4(k2+3k+2)=1>0,
∴方程有两个不相等的实数根.
(2)∵x1+x2=2k+3,x1•x2=k2+3k+2,
∴由(x1-1)(x2-1)=5,得
x1•x2-(x1+x2)+1=5,即k2+3k+2-2k-3+1=5,
整理,得
k2+k-5=0,
解得k=$\frac{-1±\sqrt{21}}{2}$;
(3)∵x2-(2k+3)x+k2+3k+2=(x-k-1)(x-k-2)=0,
∴x1=k+1,x2=k+2.
①不妨设AB=k+1,AC=k+2,
∴斜边BC=5时,有AB2+AC2=BC2,即(k+1)2+(k+2)2=25,
解得:k1=2,k2=-5(舍去).
∴当k=2时,△ABC是直角三角形
②∵AB=k+1,AC=k+2,BC=5,由(1)知AB≠AC,
故有两种情况:
(Ⅰ)当AC=BC=5时,k+2=5,
∴k=3,AB=3+1=4,
∵4、5、5满足任意两边之和大于第三边,
∴此时△ABC的周长为4+5+5=14;
(II)当AB=BC=5时,k+1=5,
∴k=4,AC=k+2=6,
∵6、5、5满足任意两边之和大于第三边,
∴此时△ABC的周长为6+5+5=16.
综上可知:当k=3时,△ABC是等腰三角形,此时△ABC的周长为14;当k=4时,△ABC是等腰三角形,此时△ABC的周长为16.
点评 本题考查了根的判别式、因式分解法解一元二次方程以及等腰三角形的判定,熟练掌握“当根的判别式△>0时,方程有两个不等实数根.”是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
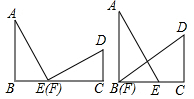 (1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF,请你证明:a2+b2=c2;
(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF,请你证明:a2+b2=c2;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
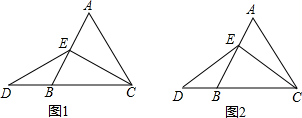
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
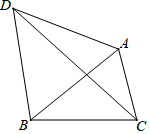 如图所示,△ABC为锐角三角形,以AB为边在△ABC的外边作等边△ABD,连结CD,若△ACD绕着点A逆时针旋转60°,试解答下列问题.
如图所示,△ABC为锐角三角形,以AB为边在△ABC的外边作等边△ABD,连结CD,若△ACD绕着点A逆时针旋转60°,试解答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com