
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 ①根据余角的定义可得出①不正确;②根据对顶角的定义可得出②不正确;③将-0.00041用科学计数法表示出来,可得出③正确;④由“在同一平面内,垂直于同一直线的两直线互相平行”,可得出④不正确;⑤根据平行线的性质“两直线平行,同旁内角互补”结合角平分线的定义,可得出⑤正确;⑥由“两边和其中一边上的中线对应相等的两个三角形全等”,可得出⑥不正确;⑦根据余角的定义,可得出⑦不正确;⑧根据补角的定义,可得出⑧正确.综上即可得出结论.
解答 解:①∵只有锐角才有余角,
∴①不正确;
②∵如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,
∴②不正确;
③∵-0.00041=-4.1×10-4,
∴③正确;
④∵在同一平面内,平行于同一直线的两直线平行,垂直于同一直线的两直线也平行,
∴④不正确;
⑤∵两直线平行,同旁内角互补,
∴同旁内角的平分线互相垂直,⑤正确;
⑥∵两边和其中一边上的中线对应相等的两个三角形全等,
∴⑥不正确;
⑦∵如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角,
∴⑦不正确;
⑧∵钝角大于它的补角,
∴⑧正确,
故选A.
点评 本题考查了全等三角形的性质、科学计数法、余角和补角、平行公理及推论以及平行线的性质,逐一分析8条结论的正误是解题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
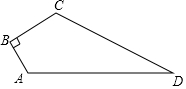 某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.
某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
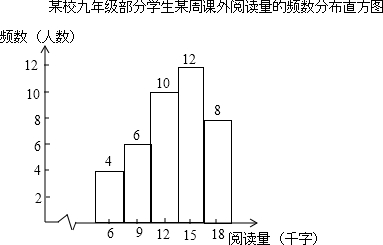 为了解九年级学生每周的课外阅读情况,某校语文组调查了该校九年级部分学生某周的课外阅读量(精确到千字),将调查数据经过统计整理后,得到如下频数分布直方图.请根据该频数分布直方图,回答下列问题:
为了解九年级学生每周的课外阅读情况,某校语文组调查了该校九年级部分学生某周的课外阅读量(精确到千字),将调查数据经过统计整理后,得到如下频数分布直方图.请根据该频数分布直方图,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
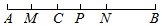 如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com