
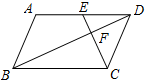
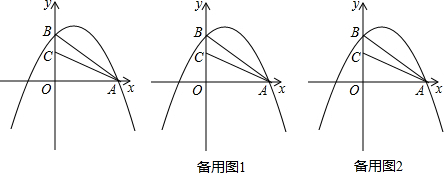
 如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.
如图,平行四边形ABCD中,点E是AD边上一点,且 CE⊥BD于点F,将△DEC沿从D到A的方向平移,使点D与点A重合,点E平移后的点记为G.分析 (1)由四边形ABCD是平行四边形,得出AD∥BC,AD=BC,将△DEC沿从D到A的方向平移,使点D与点A重合,则C与B重合,延长DA到G,使AG=DE,连结BG,则△AGB为所求;
(2)由平移的性质可得BG=CE=3,BG∥CE,而CE⊥BD,得出BG⊥BD.在Rt△BDG中利用勾股定理求出DG的长,进而得到AG的长.
解答 解:(1)△AGB为△DEC平移后的三角形,如下图所示;
(2)∵△AGB为△DEC平移后的三角形,
∴BG=CE=3,BG∥CE,
∵CE⊥BD,
∴BG⊥BD.
在Rt△BDG中,∵∠GBD=90°,BG=3,BD=6,
∴DG=$\sqrt{B{G}^{2}+B{D}^{2}}$=3$\sqrt{5}$,
∵四边形ABCD是平行四边形,
∴AD=BC=2$\sqrt{5}$,
∴AG=DG-AD=3$\sqrt{5}$-2$\sqrt{5}$=$\sqrt{5}$.
点评 本题考查了作图-平移变换,平移的性质,平行四边形的性质,作出点E平移后的点G是解题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:
某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
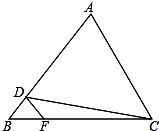 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
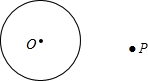 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
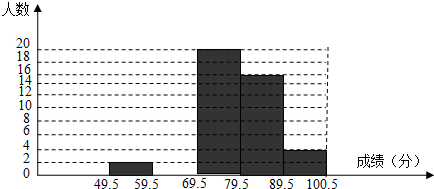
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | A | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | B | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
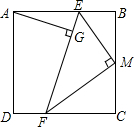 已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.
已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com