
| 3 |
| 3 |
| 3 |
| 3 |
| 12n |
科目:初中数学 来源: 题型:阅读理解
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
|
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 10 |
| 3 |
| 10 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
阅读下列材料并解决有关问题:
我们知道: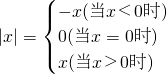 ,现在我们可以用这一结论来解含有绝对值的方程.例如,解方程|x+1|+|2x-3|=8时,可令x+1=0和2x-3=0,分别求得x=-1和,(称-1和
,现在我们可以用这一结论来解含有绝对值的方程.例如,解方程|x+1|+|2x-3|=8时,可令x+1=0和2x-3=0,分别求得x=-1和,(称-1和 分别为|x+1|和|2x-3|的零点值),在实数范围内,零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况:①x<-1②
分别为|x+1|和|2x-3|的零点值),在实数范围内,零点值x=-1和可将全体实数分成不重复且不遗漏的如下3种情况:①x<-1②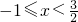 ③
③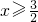 ,从而解方程|x+1|+|2x-3|=5可分以下三种情况:
,从而解方程|x+1|+|2x-3|=5可分以下三种情况:
①当x<-1时,原方程可化为-(x+1)-(2x-3)=8,解得x=-2.
②当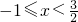 时,原方程可化为(x+1)-(2x-3)=8,解得x=-4,但不符合
时,原方程可化为(x+1)-(2x-3)=8,解得x=-4,但不符合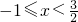 ,故舍去.
,故舍去.
③当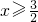 时,原方程可化为(x+1)+(2x-3)=8,解得
时,原方程可化为(x+1)+(2x-3)=8,解得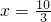 .
.
综上所述,方程|x+1|+|2x-3|=8的解为,x=-2和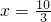 .
.
通过以上阅读,请你解决以下问题:
(1)分别求出|x+2|和|3x-1|的零点值.
(2)解方程|x+2|+|3x-1|=9.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com