
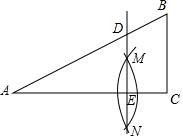
 如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.
如图,在△ABC中,∠ACB=90°,以点A为圆心,以某一长度为半径画弧,再以点C为圆心,以另一长度为半径画弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E.求证:DE∥BC.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{\frac{x+1}{3}≤1}\\{2-(x-1)<4}\end{array}\right.$,并把不等式组的解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{\frac{x+1}{3}≤1}\\{2-(x-1)<4}\end{array}\right.$,并把不等式组的解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
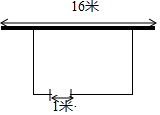 现有32米长的栅栏在长16米的墙边围成面积为130平方米的一个矩形的堆料场.在墙的对面的一边留出1米宽的进出口(如图).这个矩形的长和宽各是多少米?
现有32米长的栅栏在长16米的墙边围成面积为130平方米的一个矩形的堆料场.在墙的对面的一边留出1米宽的进出口(如图).这个矩形的长和宽各是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
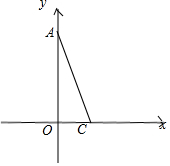 如图,△ABC在平面坐标系内,点A(0,3$\sqrt{3}$),C(2,0).点B为y轴上动点,求$\frac{1}{2}$AB+BC的最小值.
如图,△ABC在平面坐标系内,点A(0,3$\sqrt{3}$),C(2,0).点B为y轴上动点,求$\frac{1}{2}$AB+BC的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
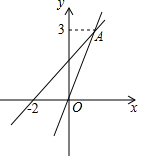 已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);
已知正比例函数y=mx与一次函数y=ax+b的图象交于点A(1,3);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com