已知抛物线y=3x2+2x+n,
(1)若n=-1,求该抛物线与x轴的交点坐标;
(2)当-1<x<1时,抛物线与x轴有且只有一个公共点,求n的取值范围.
分析:(1)把n=-1,y=0代入抛物线解析式,通过解一元二次方程可求得交点坐标.
(2)分3种情况.第1种:△=0,n=
;
第2种:把x=-1代入函数使y大于0,且把x=1代入函数,使y小于0,解这个不等式,可得n的取值范围;
第3种:把x=-1代入函数使y小于0,且把x=1代入函数,使y大于0,解这个不等式组,可得n的取值范围.
综合这三个结果即可得n的范围.在2,3种情况下必须保证△大于0.
解答:解:(1)当n=-1时,抛物线为y=3x
2+2x-1,
方程3x
2+2x-1=0的两个根为:x=-1或x=
.
∴该抛物线与x轴交点的坐标是(-1,0)和(
,0);(2分)
(2)∵抛物线与x轴有公共点,
∴对于方程3x
2+2x+n=0,判别式△=4-12n≥0,
∴n≤
.(3分)
①当n=
时,由方程3x
2+2x+
=0,解得x
1=x
2=-
.此时抛物线为y=3x
2+2x+
与x轴只有一个公共点(
-,0);(4分)
②当n<
时,
x
1=-1时,y
1=3-2+n=1+n;
x
2=1时,y
2=3+2+n=5+n;
由已知-1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为x=-
,
应有y
1≤0,且y
2>0即1+n≤0,且5+n>0.(5分)
解得:-5<n≤-1.(6分)
综合①,②得n的取值范围是:n=
或-5<n≤-1.(7分)
点评:考查二次函数y=ax2+bx+c的图象与x轴交点的个数的判断.



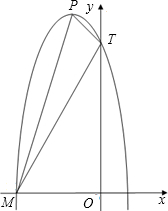 如图,已知抛物线y=-3x2-(2c-b)x+a2,其中a、b、c是一个直角三角形的三边的长,且a<b<c,又知这个三角形两锐角的正弦值分别是方程25x2-35x+12=0的两个根.
如图,已知抛物线y=-3x2-(2c-b)x+a2,其中a、b、c是一个直角三角形的三边的长,且a<b<c,又知这个三角形两锐角的正弦值分别是方程25x2-35x+12=0的两个根. 如图,已知抛物线y1=-3x2+3,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:
如图,已知抛物线y1=-3x2+3,直线y2=3x+3,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断: