
 如图,在直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标是A(-1,0),B(0,-$\frac{1}{2}$),D(0,2)
如图,在直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标是A(-1,0),B(0,-$\frac{1}{2}$),D(0,2)分析 (1)作CE⊥OD于E,则∠CED=90°,由题意得出OA=1,OB=$\frac{1}{2}$,OD=2,由平行四边形的性质得出CD=AB,CD∥AB,由AAS证明△CDE≌△ABO,得出CE=AO=1,DE=OB=$\frac{1}{2}$,得出OE=OD-DE=$\frac{3}{2}$,即可得出点C的坐标;求出$\frac{OB}{OA}$=$\frac{OA}{OD}$,证明△AOB∽△DOA,得出对应角相等∠ABO=∠DAO,再由角的互余关系得出∠BAD=90°,即可得出结论;
(2)直接把C点坐标代入反比例函数的解析式,求出k的值即可.
解答 解:(1)平行四边形ABCD是矩形.
理由:作CE⊥OD于E,如图所示: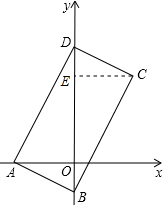 则∠CED=90°=∠AOB,
则∠CED=90°=∠AOB,
∵A(-1,0),B(0,-$\frac{1}{2}$),D(0,2),
∴OA=1,OB=$\frac{1}{2}$,OD=2,
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠CDE=∠ABO,
在△CDE和△ABO中,
∵$\left\{\begin{array}{l}∠CED=∠AOB\\∠CDE=∠ABO\\ CD=AB\end{array}\right.$,
∴△CDE≌△ABO(AAS),
∴CE=AO=1,DE=OB=$\frac{1}{2}$,
∴OE=OD-DE=2-$\frac{1}{2}$=$\frac{3}{2}$,
∴点C的坐标为(1,$\frac{3}{2}$).
∵$\frac{OB}{OA}$=$\frac{1}{2}$,$\frac{OA}{OD}$=$\frac{1}{2}$,
∴$\frac{OB}{OA}$=$\frac{OA}{OD}$,
又∵∠AOB=∠DOA=90°,
∴△AOB∽△DOA,
∴∠ABO=∠DAO,
∵∠ABO+∠BAO=90°,
∴∠DAO+∠BAO=90°,即∠BAD=90°,
∴?ABCD是矩形.
(2)∵点C的坐标为(1,$\frac{3}{2}$),
∴k=1×$\frac{3}{2}$=$\frac{3}{2}$.
点评 本题考查了反比例函数图象上点的坐标特点、矩形的判定与性质、坐标与图形性质、平行四边形的性质、全等三角形的判定与性质、相似三角形的判定与性质,本题综合性强,有一定难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
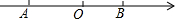 如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0.
如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b-2)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某公司今年1到4月份的总产值相对上个月的增长率统计图,下列说法:
如图是某公司今年1到4月份的总产值相对上个月的增长率统计图,下列说法:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com