
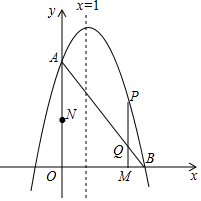
 ��ͼ����֪������y=-x2+bx+c��y���ཻ�ڵ�A��0��3������x�������ཻ�ڵ�B���Գ�����ֱ��x=1
��ͼ����֪������y=-x2+bx+c��y���ཻ�ڵ�A��0��3������x�������ཻ�ڵ�B���Գ�����ֱ��x=1���� ��1���ɶԳ��ṫʽ�����b����A����������c�������������߽���ʽ������y=0�����B�����ꣻ
��2������t�ɱ�ʾ��ON��OM����ɱ�ʾ��P�����꣬���ɱ�ʾ��PM�ij����ɾ��ε����ʿɵ�ON=PM���ɵõ�����t�ķ��̣������t��ֵ�����������֪OB=OA���ʵ���BOQΪ����������ʱ��ֻ����OB=BQ��OQ=BQ����t�ɱ�ʾ��Q������꣬��ɱ�ʾ��OQ��BQ�ij����ֱ�õ�����t�ķ��̣������t��ֵ��
��� �⣺
��1����������y=-x2+bx+c�Գ�����ֱ��x=1��
��-$\frac{b}{2����-1��}$=1�����b=2��
�������߹�A��0��3����
��c=3��
�������߽���ʽΪy=-x2+2x+3��
��y=0�ɵ�-x2+2x+3=0�����x=-1��x=3��
��B��������3��0����
��2�����������֪ON=3t��OM=2t��
��P���������ϣ�
��P��2t��-4t2+4t+3����
���ı���OMPNΪ���Σ�
��ON=PM��
��3t=-4t2+4t+3�����t=1��t=-$\frac{3}{4}$����ȥ����
�൱t��ֵΪ1ʱ���ı���OMPNΪ���Σ�
�ڡ�A��0��3����B��3��0����
��OA=OB=3���ҿ����ֱ��AB����ʽΪy=-x+3��
�൱t��0ʱ��OQ��OB��
�൱��BOQΪ����������ʱ����OB=QB��OQ=BQ���������
�������֪OM=2t��
��Q��2t��-2t+3����
��OQ=$\sqrt{��2t��^{2}+��-2t+3��^{2}}$=$\sqrt{8{t}^{2}-12t+9}$��BQ=$\sqrt{��2t-3��^{2}+��-2t+3��^{2}}$=$\sqrt{2}$|2t-3|��
���������֪0��t��1��
��OB=QBʱ������$\sqrt{2}$|2t-3|=3�����t=$\frac{6+3\sqrt{2}}{4}$����ȥ����t=$\frac{6-3\sqrt{2}}{4}$��
��OQ=BQʱ������$\sqrt{8{t}^{2}-12t+9}$=$\sqrt{2}$|2t-3|�����t=$\frac{3}{4}$��
���Ͽ�֪��t��ֵΪ$\frac{6-3\sqrt{2}}{4}$��$\frac{3}{4}$ʱ����BOQΪ���������Σ�
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������ε����ʡ����ɶ��������������ε����ʡ�����˼�뼰��������˼���֪ʶ���ڣ�1����ע�����ϵ������Ӧ�ã��ڣ�2��������t��ʾ��PM��ON�ij��ǽ���Ĺؼ����ڢ�����t��ʾ��Q������꣬������ʾ��OQ��BQ�ij��ǽ���Ĺؼ���ע���������ۣ����⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 55 | B�� | 56 | C�� | 57 | D�� | 58 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ��Ա | �� | �� | �� | �� | �� | ����/��2 | ƽ���ɼ�/�� |
| �ɼ�/�� | 81 | 79 | �� | 80 | 82 | �� | 80 |
| A�� | 80��2 | B�� | 80��10 | C�� | 78��2 | D�� | 78��10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2•a2=2a2 | B�� | a2+a2=a4 | C�� | ��1+2a��2=1+2a+4a2 | D�� | ��-a+1����a+1��=1-a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
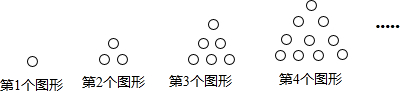
| A�� | 11 | B�� | 12 | C�� | 13 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com