
| 班级 | 参加人数 | 中位数 | 方差 | 平均数 |
| (1)班 | 50 | 120 | 103 | 122 |
| (2)班 | 49 | 121 | 201 | 122 |
| A. | 两班平均成绩一样 | B. | (1)班的优秀人数多于(2)班 | ||
| C. | (2)班的两极分化比(1)班严重 | D. | (1)班的总体成绩稳定一些 |
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
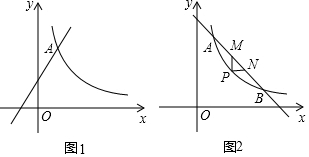
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
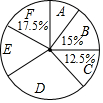 某中学将为初一学生开设A、B、C、D、E、F6种运动项目,现选取部分学生进行了“我最喜欢的一种运动项目”调查,将调查结果绘制成如下统计图表(不完整),根据图表提供的信息,下列判断中,不正确的是( )
某中学将为初一学生开设A、B、C、D、E、F6种运动项目,现选取部分学生进行了“我最喜欢的一种运动项目”调查,将调查结果绘制成如下统计图表(不完整),根据图表提供的信息,下列判断中,不正确的是( ) | 运动项目名称 | A | B | C | D | E | F |
| 人数 | 40 | 60 | 100 |
| A. | 这次被调查的学生认识400人 | |
| B. | 扇形统计图中D部分扇形的圆心角为90° | |
| C. | 被调查的学生中喜欢运动项目E的人数为80 | |
| D. | 喜欢运动项目C的人数最少 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
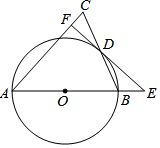 如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.
如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
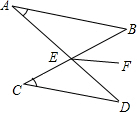 如图,已知AB∥CD,AD与BC相交于点E,EF平分∠BED,若∠A=30°,∠C=40°,则∠DEF的度数为( )
如图,已知AB∥CD,AD与BC相交于点E,EF平分∠BED,若∠A=30°,∠C=40°,则∠DEF的度数为( )| A. | 70° | B. | 50° | C. | 35° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com